Anmerkung: Dieses Kapitel ist angelehnt an das Skript Quantenmechanik von Horst Rollnik, III. Kapitel, Vorlesung gehalten im WS 1975/76 an der Universität Bonn, sowie an Feynman: Vorlesungen über Physik, Band III: Quantenmechanik, Kapitel 5.
Wer die Quantentheorie an der Universität lernt, der wird nach den Begriffen Wellenfunktion und Schrödingergleichung schon bald etwas über Hilberträume, Eigenzustände und Operatoren hören. Nach meiner Erfahrung bekommt man diesen mathematischen Apparat zumeist als Gesamtpaket einfach serviert, ohne dass klar wird, warum man ausgerechnet diese Mathematik hier verwenden kann.
Wir sind in den vorherigen Kapiteln etwas anders vorgegangen und haben Begriffe wie Schrödingergleichung und Wellenfunktion bewusst zurückgestellt. Der Grund dafür liegt darin, dass Wellenfunktionen und die übliche Schrödingergleichung nur in einem bestimmten Bereich der Quantentheorie anwendbar sind: in der nichtrelativistischen Quantenmechanik und dabei speziell in der Atomphysik. Die von uns verwendeten Wahrscheinlichkeitsamplituden und die bisher besprochenen Regeln für ihre Anwendung sind dagegen in der gesamten Quantentheorie anwendbar und gelten auch in der relativistischen Quantenfeldtheorie.
Bisher haben wir jedoch erst einige Grundeigenschaften von Wahrscheinlichkeitsamplituden kennengelernt und es ist nun an der Zeit, konkreter zu werden und den gesamten mathematischen Apparat der Quantentheorie schrittweise aufzubauen. Dabei wollen wir darauf achten, dass die so entwickelte mathematische Struktur für die gesamte Quantentheorie gilt (und nicht nur für die nichtrelativistische Quantenmechanik).
Beginnen wir mit dem Begriff des quantenmechanischen Zustandes eines Systems.
Dieser Begriff hängt eng mit dem Begriff vollständiges Ereignis zusammen, den wir bereits in Kapitel 4.2 verwendet haben. Wir hatten dazu gesagt, dass ein solches Ereignis alle Informationen umfassen muss, die in der Natur vorliegen. Genauer müssten wir sagen, dass ein solches Ereignis durch einen vollständigen Satz miteinander verträglicher Messwerte festgelegt wird. Nur einem solchen Ereignis darf man eine Wahrscheinlichkeitsamplitude zuordnen.
Was aber bedeuten die Begriffe vollständig und verträglich in diesem Zusammenhang?
Vollständig heißt, dass wir nicht mehr Informationen über das System gewinnen können, oder aber dass solche zusätzlichen Informationen (z.B. der innere Aufbau eines Elementarteilchens) für das betrachtete Experiment nicht relevant sind, da die damit zusammenhängenden physikalischen Freiheitsgrade nicht berührt werden (beispielsweise ist die innere Struktur des Atomkerns bei chemischen Experimenten nicht relevant, da die chemischen Energien viel zu niedrig sind, um den Atomkern zu beeinflussen).
Dabei ist es keineswegs einfach, zu wissen, ob die gemessenen Informationen in diesem Sinn vollständig sind. Die Untersuchung dieser Frage ist vielmehr im Allgemeinen Gegenstand der physikalischen Forschung.
Kommen wir zu dem Begriff verträglich. Die Messungen müssen miteinander verträglich sein, d.h. die Messung der einen Messgröße verändert nicht den Wert einer damit verträglichen anderen Messgröße. So ist es immer möglich, Ort und Spin eines Elektrons zu messen. Es ist ebenfalls immer möglich, Impuls und Spin eines Elektrons zu messen, d.h. man kann den Impuls messen, ohne eine zuvor gemessene Spininformation zu verlieren.
Gibt es auch Messungen, die nicht miteinander verträglich sind? Ja, die gibt es! Beispielsweise zerstört die Messung des Ortes an einem Teilchen die Information über seinen Impuls. Und genauso zerstört die Messung der Spinkomponente eines Elektrons in z-Richtung die Information über die Spinkomponente in x- oder y-Richtung.
Als Folge davon gibt es verschiedene Möglichkeiten für einen vollständigen Satz miteinander verträglicher Messwerte. Für ein Elektron könnte man beispielsweise Ort und Spin in z-Richtung oder Ort und Spin in x-Richtung oder Impuls und Spin in z-Richtung wählen.
Nun sind wir gerüstet, den quantenmechanischen Zustandes eines Systems zu definieren:
Wir sagen, dass sich ein physikalisches System in einem bestimmten quantenmechanischen Zustand befindet, wenn ein vollständiger Satz von (miteinander verträglichen) Messwerten über das System bekannt ist.
Der Zustand wird also durch Angabe dieser Messwerte eindeutig gekennzeichnet. Nur solange diese Information noch gültig ist, d.h. nur solange sich die Messwerte reproduzieren lassen, können wir sagen, dass sich das System noch in diesem Zustand befindet.
Wie aber kommen wir zu einem vollständigen Satz von Messwerten? Entweder, wir wissen aus irgendwelchen Gründen bereits genug über das System (z.B. aufgrund seiner Entstehung), oder aber wir müssen die Werte explizit an dem physikalischen System messen und dadurch einen solchen Zustand erst herstellen. Man sagt auch, dass man einen quantenmechanischen Zustand durch Messung präpariert. Erst nach dieser Messung befindet sich das System also in dem entsprechenden Zustand.
Ein Beispiel: In unserem Doppelspaltexperiment haben wir angenommen, dass die Teilchenquelle einen Strahl Elektronen mit einem bestimmten Impuls aussendet. Weiterhin wollen wir annehmen, dass nur Elektronen mit Spin in z-Richtung erzeugt werden. Solche Elektronen könnten wir z.B. mit einem inhomogenen Magnetfeld herausfiltern. Da Impuls und Spinkomponente zusammen einen vollständigen Satz von Messwerten bilden (das müssen Sie mir an dieser Stelle einfach mal ohne weitere Begründung glauben), können wir sagen, dass sich diese Elektronen vor dem Doppelspalt in einem quantenmechanischen Zustand befinden, der durch einen bestimmten Impuls und eine bestimmte Spinkomponente gekennzeichnet ist.
Wir wollen an dieser Stelle nach dem Vorbild Paul Diracs eine Schreibweise für einen solchen Zustand einführen: wir schreiben alle Messwerte einfach in gewissen Klammern (genauer: ein senkrechter Strich und eine Winkelklammer) hintereinander. Den Elektronzustand mit Impuls \(\boldsymbol{p}\) und Spinkomponente \(m_z\) in z-Richtung schreiben wir also als \[ | \boldsymbol{p}, m_z \rangle \] Warum diese merkwürdige Klammerschreibweise praktisch ist, werden wir etwas später noch sehen.
Einen allgemeinen Zustand irgendeines physikalischen Systems werden wir analog als \[ | \psi \rangle \] oder \[ | \phi \rangle \] etc. schreiben. Dabei stehen die griechischen Buchstaben einfach für eine vollständige Liste entsprechender Messwerte, so wie sie für das betrachtete System messbar sind.
Es ist hier noch völlig unklar, was für ein mathematisches Objekt wir mit einem Zustand identifizieren können, da wir noch keine weiteren Regeln aufgestellt haben, wie mit solchen Zuständen umzugehen ist.
Um zu solchen Regeln zu kommen, müssen wir überlegen, welche Verbindung zwischen einem solchen Zustand und den Wahrscheinlichkeitsamplituden für ein experimentelles Ereignis besteht. Ein solches Ereignis wäre bei unserem Doppelspaltexperiment das Auftreffen eines Elektrons auf dem Leuchtschirm hinter dem Doppelspalt.
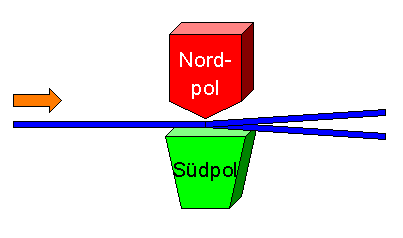
Für die Entwicklung der folgenden Ideen ist es allerdings besser, ein einfacheres Beispiel zu verwenden. Wir betrachten dazu einen Strahl elektrisch neutraler Fermionen (also Spin-1/2-Teilchen, z.B. Neutronen), der in x-Richtung mit festem Impuls \(\boldsymbol{p}\) fliegt.
Dieser Strahl kann auf seinem Weg ein oder
mehrere inhomogene Magnetfelder durchfliegen.
Die Magnetfelder sind dabei in y- oder z-Richtung orientiert.
Da das Neutron Spin 1/2 besitzt, teilt sich der Strahl
beim Durchfliegen eines in z-Richtung orientierten Magnetfeldes
in zwei Teilstrahlen auf. Der eine Teilstrahl wird leicht nach oben
(also in z-Richtung),
der andere leicht nach unten (also gegen die z-Richtung) abgelenkt.

Jedem der beiden Teilstrahlen entspricht ein bestimmter Wert der Spinkomponente in z-Richtung, die wir als \(m_z\) bezeichnet haben. Im einen Teilstrahl ist \(m_z = 1/2\), im anderen Teilstrahl ist \(m_z = - 1/2\). Warum der Wert gerade 1/2 ist, können wir hier noch nicht verstehen. Wichtig ist im Moment nur, dass es zwei Messwerte gibt, und dass der Messwert durch die Zugehörigkeit zum einen oder anderen Teilstrahl festgelegt ist. Durch das Auffinden eines Teilchens in einem der beiden Teilstrahlen wird der Wert von \(m_z\) also gemessen.
Wir wollen weiterhin annehmen, dass die Ablenkung im Magnetfeld so gering ist, dass wir auch danach noch von Strahlen sprechen können, die im Wesentlichen in x-Richtung fliegen (ansonsten könnten wir sie eben nach der Trennung noch ein klein wenig umlenken, bis sie wieder in x-Richtung fliegen - wir wollen den Apparat aber nicht zu kompliziert machen).
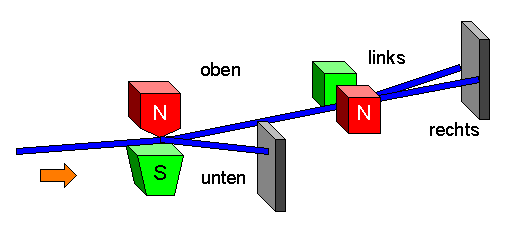
Betrachten wir nun ein in y-Richtung orientiertes inhomogenes Magnetfeld. Auch hier teilt sich der Strahl beim Durchgang in zwei Teilstrahlen auf. Der eine Teilstrahl wird leicht nach links (also in y-Richtung), der andere leicht nach rechts (also gegen die y-Richtung) abgelenkt. Jedem der beiden Teilstrahlen entspricht ein bestimmter Wert der Spinkomponente \(m_y\) in y-Richtung. Im einen Teilstrahl ist \(m_y = 1/2\), im anderen Teilstrahl ist \(m_y = - 1/2\).
Betrachten wir nun folgende Situation:
Der Strahl fliegt in x-Richtung durch ein Magnetfeld, das in z-Richtung steht, und wir blockieren den Weg eines der beiden Teilstrahlen hinter dem Magneten, so dass nur ein Teilstrahl übrig bleibt. Damit wissen wir, welchen Wert die Spinkomponente \(m_z\) hat. Der Impuls hat sich beim Durchgang durch das Magnetfeld nicht geändert (die kleine Ablenkung wollten wir dabei ja vernachlässigen). Impuls und Spinkomponente bilden für Fermionen einen vollständigen Satz von Messwerten, solange die Energien so klein sind, dass eine Substruktur der Teilchen keine Rolle spielt (das sei hier der Fall). Wir können daher sagen, dass sich die Teilchen in diesem durchgelassenen Teilstrahl im quantenmechanischen Zustand \( | \boldsymbol{p}, m_z \rangle \) befinden. Diesen Zustand haben wir mit Hilfe des Magnetfeldes also präpariert.
Wir wollen nun diesen Teilstrahldurch einen weiteren Magneten schicken, dessen Magnetfeld in y-Richtung orientiert ist. Auch hier teilt sich der Strahl wiederum in zwei Teilstrahlen auf, die durch \(m_y = +1/2\) bzw. \(m_y = -1/2\) gekennzeichnet sind. Der Impuls wird dabei (zumindest in guter Näherung) nicht verändert.
Sobald wir wissen, in welchem der beiden Teilstrahlen sich ein Teilchen befindet, kennen wir den Wert seiner Spinkomponente \(m_y\) , d.h. in diesem Moment haben wir sie gemessen. Das zur Messung gehörende Ereignis lautet also: Finde das Teilchen in einem der beiden Teilstrahlen. Es handelt sich dabei um ein vollständiges Ereigniss, denn
Dies ist im Grunde unsere erste wirklich präzise Formulierung
des Begriffs vollständiges Ereignis.
Da es sich um vollständige Ereignisse handelt, können wir jedem dieser Ereignisse eine Wahrscheinlichkeitsamplitude zuordnen, deren Betragsquadrat die Wahrscheinlichkeit dafür angibt, dass das Ereignis eintritt. Diese Amplitude hängt zum einen natürlich von den gefundenen Messwerten ab, also von \(\boldsymbol{p}\) und \(m_y\). Sie hängt aber auch von dem Zustand ab, an dem die Messung durchgeführt wurde, also von \(\boldsymbol{p}\) und \(m_z\) . Ein Strahl mit \(m_z = 1/2\) muss sich beim Durchgang durch das in y-Richtung orientierte Magnetfeld ja nicht unbedingt genauso verhalten wie ein Strahl mit \(m_z = -1/2\) (die Abhängigkeit vom Impuls \(\boldsymbol{p}\) haben wir hier nur der Vollständigkeit mitgenommen).
Wir schreiben daher die Amplitude als \[ A(\boldsymbol{p}, m_y, \boldsymbol{p}, m_z) \] Dabei wollen wir die Messwerte, die den vorliegenden Zustand vor der Messung charakterisieren, rechts schreiben, und die Messwerte, die bei der Messung gefunden werden, links schreiben. Diese Reihenfolge wird sich später noch als nützlich erweisen.
Im allgemeinen Fall schreiben wir analog \[ A(\phi, \psi) \] für die Wahrscheinlichkeitsamplitude, dass an einem System im Zustand \( |\psi \rangle \) in dem betrachteten Experiment die Messwerte von \( |\phi \rangle \) gemessen werden, so dass sich das System unmittelbar nach der Messung im Zustand \( |\phi \rangle \) befindet.
Übrigends: Natürlich muss \[ |A(\psi, \psi)|^2 = 1 \] sein, denn wir wissen über das System ja, dass es sich vor der Messung bereits im Zustand \( |\psi \rangle \) befindet, und das bedeutet, dass wir bei einer erneuten Messung derselben physikalischen Größen wieder dieselben finden werden, die \( |\psi \rangle \) charakterisieren.
Noch eine Randbemerkung: Die Spinkomponenten \(m_z\) und \(m_y\) (und allgemeiner die Messwertlisten \( |\psi \rangle \) und \( |\phi \rangle \) ) beinhalten implizit auch immer die Angabe einer Messvorschrift, denn man muss ja auch sagen, für welches Experiment man die Wahrscheinlichkeitsamplituse angibt. Die Amplitude \( A(\boldsymbol{p}, m_y, \boldsymbol{p}, m_z) \) gilt also für ein Experiment, bei dem ein Teilchenstrahl mit Impuls \(\boldsymbol{p}\) durch ein inhomogenes Magnetfeld in z-Richtung herausgefiltert wird, und an diesem Teilstrahl anschließend eine Messung mit einem inhomogenen Magnetfeld in y-Richtung durchgeführt wird. Das meint man, wenn man sagt, man findet einen gewissen Satz von Messwerten. Dazu muss eine experimentelle Anordnung gehören, die genau diese Messung (z.B. y-Komponente des Spins) ermöglicht. Mit einem Magnetfeld, dass die y-Spinkomponente misst, kann man nicht gleichzeitig die z-Komponente messen, denn dafür müsste das Magnetfeld anders orientiert sein.
Für die folgende Diskussion wollen wir nun eine Sprachregelung vereinbaren: Wir bezeichnen ab sofort einen Magneten mit in y-Richtung orientiertem inhomogenen Magnetfeld als y-Magneten. Analog definieren wir einen z-Magneten.
Im oben betrachtete Fall hatten wir also mit einem z-Magneten einen Teilstrahl mit eindeutigem \(m_z\) herausgepickt und diesen durch einen y-Magneten geschickt. Picken wir nun hinter dem y-Magneten erneut einen Teilstrahl heraus, so hat dieser nun einen eindeutigen Wert für \(m_y\). Zu dieser Messung gehört die Wahrscheinlichkeitsamplitude \[ A(\boldsymbol{p}, m_y, \boldsymbol{p}, m_z) \] Nun könnten wir dahinter wieder einen z-Magneten aufstellen und an dem herausgefilterten Strahl mit festem \(m_y\)-Wert wieder die Wahrscheinlichkeit für \(m_z\) messen. Zu dieser Messung gehört nun die Wahrscheinlichkeitsamplitude \[ A(\boldsymbol{p}, m_z , \boldsymbol{p}, m_y) \] Dabei zeigt sich: Es ist völlig egal, aus welchem ursprünglichen \(m_z\)-Strahl die Teilchen stammen. Wichtig ist allein, aus welchem \(m_y\)-Strahl die Teilchen sind. Das Herausfiltern eines \(m_y\)-Strahls hat die ursprüngliche Information über \(m_z\) komplett ausgelöscht, oder besser: es hat sie ersetzt. Die Teilchen in den beiden \(m_y\)-Strahlen scheinen jede Erinnerung an ihren früheren \(m_z\)-Wert verloren zu haben
Nun verändern wir diese Versuchsanordnung etwas: Hinter dem ersten z-Magneten blockieren wir weiterhin einen der beiden Teilstrahlen, so dass wir einen eindeutigen Wert für \(m_z\) haben. Dann lassen wir diesen durchgelassenen Teilstrahl wie bisher durch einen y-Magneten laufen. Der Strahl teilt sich also erneut in zwei Teilstrahlen mit \(m_y = 1/2\) und \(m_y = - 1/2\) auf. Diesmal jedoch blockieren wir keinen dieser beiden Teilstrahlen, sondern wir führen sie hinter dem Magneten wieder zu einem einzigen Strahl zusammen (z.B. mit Hilfe eines geeigneten Magnetfeldes). Den zusammengeführten Strahl schicken wir dann wieder durch einen z-Magneten, der nochmal Wert von \(m_z\) bestimmt.
Wie lautet nun unser experimentelles Ergebnis? Die Antwort ist: der letzte z-Magnet misst genau den \(m_z\)-Wert, den wir hinter dem ersten z-Magneten herausgefiltert haben. Der Durchgang durch den y-Magneten, die Aufteilung und anschließende Wiedervereinigung der Teilstrahlen haben den Wert von \(m_z\) nicht verändert!
Aber wie kann das sein? Hatten wir nicht eben gesagt, dass die finale Messung von \(m_z\) an einem der beiden \(m_y\)-Teilstrahlen nicht von dem ursprünglich herausgefiltertem \(m_z\)-Wert abhängt? Hatten wir nicht gesagt, dass die Messung des \(m_y\)-Wertes die Kenntnis über den vorher gemessenen \(m_z\)-Wert auslöscht bzw. ersetzt? Ja, genauso ist es!
Wo also ist der Unterschied?
Der Unterschied ist, dass wir beim Aufteilen und erneuten Zusammenführen der beiden Teilstrahlen im y-Magneten den Wert von \(m_y\) gar nicht messen! Wir wissen nur, dass die Teilchen einen der beiden Wege genommen haben, aber nicht, welchen. Die Situation ist vollkommen analog zum Doppelspaltversuch: die beiden Ablenkungsmöglichkeiten im y-Magneten entsprechen den beiden Möglichkeiten, durch einen der beiden Spalte im Doppelspaltversuch hindurchzukommen.
Die beiden beiden Ablenkungsmöglichkeiten im y-Magneten sind ununterscheidbar, solange wir nicht nachsehen, welchen Weg die Teilchen genommen haben. Entsprechend interferieren die zugehörigen Wahrscheinlichkeitsamplituden, d.h. sie müssen addiert werden.
Versuchen wir, die Wahrscheinlichkeitsamplitude \[ A(\boldsymbol{p}, m_z', \boldsymbol{p}, m_z) \] so zu schreiben, dass die Interferenz der beiden Möglichkeiten sichtbar wird. Dabei ist dies die Amplitude dafür, dass wir am Anfang einen Strahl mit definierten \(m_z\) herausfiltern, und nach dem Aufteilen und Wiedervereinigen im y-Magneten den Wert \(m_z'\) messen. Wie oben bereits gesagt, ist diese Amplitude gleich Null, wenn \(m_z' \ne m_z\) ist. Um die Notation zu vereinfachen, wollen wir den Impuls \(\boldsymbol{p}\) im Folgenden weglassen, da er für die Betrachtung keine Rolle spielt.
Die Amplitude dafür, dass ein Fermion mit definiertem \(m_z\) in einem der beiden Teilstrahl mit festem \(m_y\) aufgefunden wird, ist \[ A(m_y,m_z) \] Die Amplitude dafür, dass bei einem solchen Fermion aus einem der beiden y-Teilstrahlen anschließend der Wert \(m_z'\) gemessen wird, ist \[ A(m_z', m_y) \] Die Amplitude dafür, dass das Fermion also die Möglichkeit wählt, bei der diese beiden Schritte hintereinandergeschaltet sind, ist nach unseren Regeln für Wahrscheinlichkeitsamplitiuden das Produkt dieser beiden Amplituden, also \[ A(m_z', m_y) \, A(m_y,m_z) \] Das ist also die Amplitude dafür, dass ein Teilchen mit bekanntem \(m_z\) den \(m_y\)-Teilstrahl im y-Magneten wählt und anschließend in einem z-Magneten der Wert \(m_z'\) gemessen wird.
Wenn die beiden \(m_y\)-Alternativen ununterscheidbar sind (wir also nicht wissen, welcher y-Teilstrahl genommen wurde), dann ist die Gesamtamplitude die Summe all dieser Amplituden, also \[ A(m_z', m_z) = \sum_{m_y} A(m_z', m_y) \, A(m_y,m_z) \] Die Summe enthält hier nur zwei Summanden, nämlich den für \(m_y = 1/2\) und den für \(m_y = - 1/2\). Der Wert von \(m_y\) kennzeichnet dabei die verschiedenen ununterscheidbaren Möglichkeiten, wie das Ereignis eintreten kann.
Die obige Formel ist eine der wichtigsten Formeln der Quantentheorie. Sie gilt in ganz allgemeiner Form. So kann man beispielsweise den wiedervereinigten Strahl am Schluss durch ein inhomogenes Magnetfeld schicken, das um den Winkel \(\alpha\) gegen die z-Achse geneigt ist, und die Spinkomponente \(m_\alpha\) messen (wobei der Strahl weiterhin senkrecht auf das Magnetfeld treffen soll). Dann ist \[ A(m_\alpha, m_z) = \sum_{m_y} A(m_\alpha, m_y) \, A(m_y,m_z) \] Und man kann außerdem statt dem y-Magneten, der den Strahl zwischendurch aufteilt, einen beliebig um einen Winkel \(\beta\) gedrehten Magneten verwenden. Dann ist \[ A(m_\alpha, m_z) = \sum_{m_\beta} A(m_\alpha, m_\beta) \, A(m_\beta,m_z) \] Und die Formel ist auch richtig, wenn man Teilchen mit anderem Spin betrachtet, beispielsweise mit Spin 1. Dann treten drei Teilstrahlen auf mit \(m_y = 1, 0, -1\).
Ganz allgemein stellt sich diese Erkenntnis so dar:
Wir gehen aus von einem quantenmechanischen Zustand \( | \psi \rangle \), d.h. wir haben Kenntnis über einen vollständigen Satz von Messwerten, den diesen Zustand charakterisieren. Nun führen wir an diesem Zustand eine Messung eines (i.a. anderen) vollständigen Satzes von Messgrößen durch, die einen Zustand \( | \phi \rangle \) charakterisieren und fragen nach der zugehörigen Wahrscheinlichkeitsamplitude \[ A(\phi,\psi) \] Wenn wir die physikalische Situation analysieren, werden wir dabei zumeist feststellen, dass das Ereignis auf verschiedene Arten eintreten kann. Es handelt sich dabei um eine gedankliche Aufteilung in verschiedene Teilschritte und Alternativen. Alle diese Alternativen sind in dem betrachteten Experiment ununterscheidbar, aber man könnte das Experiment so verändern, dass man nachweisen könnte, welche Möglichkeit gewählt wurde. Bei diesem Nachweis würde allerdings die Interferenz der Amplituden, die zu den einzelnen Alternativen gehören, verloren gehen, d.h. man darf die Amplituden in diesem veränderten Experiment nicht mehr addieren.
Jede der Alternativen muss nun ebenfalls durch einen vollständigen Satz von Messwerten gekennzeichnet sein, den wir mit dem Zwischenzustand \( | n \rangle \) bezeichnen wollen (z.B. die beiden y-Teilstrahlen). Alle diese ununterscheidbaren Möglichkeiten interferieren nun zum Gesamtergebnis, d.h. es ist \[ A(\phi,\psi) = \sum_n A(\phi,n) \, A(n,\psi) \] Die Summe geht dabei über alle möglichen Messwertsätze \(n\).
Wichtig ist dabei, dass wir vollkommene Freiheit haben, die physikalischen Messgrößen \(n\) festzulegen, durch die die Aufteilung in verschiedene Alternativen erfolgt. Wichig ist nur, dass es ein vollständiger Satz von Messgrößen ist, und dass echte Alternativen vorliegen, d.h. \[ A(n,n') = 0 \] für \(n \ne n'\) und \[ |A(n,n)|^2 = 1 \]
Betrachten wir ein weiteres Beispiel: das Elektron in einem Wasserstoffatom im Grundzustand. Wir wollen annehmen, dass der Spin des Elektrons im betrachteten Experiment keine Rolle spielt. In diesem Fall besitzen wir einen vollständigen Satz von Messwerten für das Elektron: seine Energie \(E\) (Grundzustand im Wasserstoffatom). Wir bezeichnen diesen Zustand daher als \( |E \rangle \).
Wir können nun fragen: wie groß ist die Amplitude \[ A(\boldsymbol{x},E) \] dafür, das Elektron am Ort \(\boldsymbol{x}\) zu finden?
Andererseits können wir auch fragen: wie groß ist die Amplitude \[ A(\boldsymbol{p},E) \] dafür, das Elektron mit Impuls \(\boldsymbol{p}\) zu finden?
Nun lassen sich Ort und Impuls nicht gleichzeitig bestimmen (wir kommen in einem späteren Kapitel noch einmal darauf zurück). Wenn wir also nach der Amplitude \( A(\boldsymbol{x},E) \) fragen, so gibt es für den Impuls des Elektrons im Wasserstoffatom sehr viele hier ununterscheidbare Möglichkeiten, die dazu beitragen können, das Elektron am Ort \(\boldsymbol{x}\) zu finden. Es ist also \[ A(\boldsymbol{x},E) = \sum_{\boldsymbol{p}} A(\boldsymbol{x},\boldsymbol{p}) \, A(\boldsymbol{p},E) \] Dabei ist \(A(\boldsymbol{x},\boldsymbol{p})\) die Amplitude dafür, dass ein Elektron mit Impuls \(\boldsymbol{p}\) am Ort \(\boldsymbol{x}\) aufgefunden wird. Übrigens sind wir hier etwas ungenau in der Schreibweise: da der Impuls einen kontinuierlichen Wertebereich annehmen kann, müssten wir eigentlich mit Integralen arbeiten. Diese Feinheit wollen wir aber erst später beachten.
Umgekehrt ist aber auch \[ A(\boldsymbol{p},E) = \sum_{\boldsymbol{x}} A(\boldsymbol{p},\boldsymbol{x}) \, A(\boldsymbol{x},E) \] denn die einzelnen hier ununterscheidbaren Alternativen für den Ort interferieren, wenn wir nach dem Impuls fragen (auch hier müssen wir genau genommen mit Integralen arbeiten). Wir sehen, wie trickreich die ganze Angelegenheit sein kann!
Wir haben nun eine ganze Menge über Amplituden gelernt. Andererseits haben wir den Begriff quantenmechanischer Zustand eingeführt und gesehen, dass eine Amplitude von zwei solchen Zuständen abhängt: dem präparierten vor der Messung und dem, der durch die Messung wiederum präpariert wird, denn die Messung verändert ja das Wissen über das physikalische System. Wir wollen daher versuchen, unser Wissen über Amplituden in einen Formalismus für Zustände zu übersetzen. Machen wir uns also auf die Suche nach einem mathematischen Modell für Zustände.
Was muss ein solches Modell leisten? Was für ein mathematisches Objekt kann einen Zustand \( |\psi \rangle \) darstellen? Was für mathematische Eigenschaften muss dieses Objekt haben? Schauen wir uns das genauer an:
Unsere zentrale Formel für die Interferenz von Amplituden lautet \[ A(\phi,\psi) = \sum_n A(\phi,n) \, A(n,\psi) \] Man kann diese Formel auch so interpretieren: Der Zustand \( |\psi \rangle \) lässt sich aus Zuständen \( |n \rangle \) zusammensetzen bzw. in diese Zustände zerlegen (z.B. indem wir einen \(m_z\)-Strahl in mehrere \(m_y\)-Teilstrahlen aufteilen). Wir wollen diese Interpretation mathematisch durch Ausdrücke der Form \[ |\psi \rangle = \sum_n a_n \, |n \rangle \] darstellen. Dabei sollen \(a_n\) komplexe Zahlen sein, analog zu den Amplituden. Ob Ausdrücke dieser Art für unsere Zwecke brauchbar sind, ist momentan noch unklar. Wir werden es einfach schrittweise ausprobieren müssen.
Was bedeutet nun diese Addition und Multiplikation? Nun, bis zu einer physikalischen Interpretation fehlt uns noch ein Schritt. Aus formaler Sicht genügt es aber, zunächst einige Rechenregeln für diese Art der Addition und Multiplikation festzulegen.
Man braucht das Rad hier glücklicherweise nicht neu zu erfinden, denn die Mathematik hält bereits einen Baukasten bereit, der es erlaubt, mit solchen Ausdrücken umzugehen: Wir fordern, dass die Addition von \( |n \rangle \) -Objekten und deren Multiplikation mit komplexen Zahlen wie \(a_n\) den sogenannten Vektorraumaxiomen über dem Körper der komplexen Zahlen genügt. Mit anderen Worten: die gesuchten mathematischen Objekte \( |n \rangle \) sind Vektoren irgendeines Quanten-Vektorraums. Ob dieser Ansatz geeignet ist, müssen wir nun im Detail untersuchen.
Ich möchte hier nicht alles wiederholen, was es zu Vektorräumen zu sagen gibt. Hierzu gibt es bereits viele Lehrbücher. An dieser Stelle sollen nur kurz die wesentlichen Axiome angegeben werden, aus denen sich alle Rechenregeln für Vektoren herleiten:
Zur Erinnerung: diese Regeln sind Axiome, d.h. wir leiten sie nicht her, sondern wir fordern, dass sie für unsere mathematischen Zustandsobjekte wie \( |\psi \rangle \) gelten. Erst dadurch erhält z.B. das \( + \) -Symbol in unseren formalen Ausdrücken den Charakter einer Addition.
Die quantenmechanischen Zustands-Vektoren sind auch nicht mit dreidimensionalen Vektoren gleichzusetzen, die z.B. zur Beschreibung der Geschwindigkeit eines Teilchens verwendet werden. Der Begriff des Vektors ist allgemeiner, und es gibt viele mathematische Objekte, die Vektoren sind. Vektor sein heißt nur, dass die Vektorraumaxiome gelten – nicht mehr und nicht weniger.
Um zu überprüfen, ob sich dieser mathematische Formalismus zur Beschreibung von quantenmechanischen Zuständen eignet, müssen wir noch den Bezug zu den Wahrscheinlichkeitsamplituden herstellen.
Je zwei Zustände definieren eine solche Amplitude. Entsprechend bräuchte man eine mathematische Abbildung, die zwei Vektoren \( |\psi \rangle \) und \( |\phi \rangle \) eine komplexe Zahl (also die Amplitude \(A(\phi,\psi)\) ) zuordnet. Außerdem muss die Abbildung verträglich sein mit der Möglichkeit, eine Amplitude in eine Summe anderer Amplituden aufzuteilen (Interferenz der Möglichkeiten).
Eine bekannte mathematische Abbildung, die genau das leistet, ist das sogenannte (positiv definite) Skalarprodukt. Wir wollen das Skalarprodukt von zwei Vektoren \( |\psi \rangle \) und \( |\phi \rangle \) in der Form \[ \langle \phi | \psi \rangle \] schreiben. Diese Schreibweise klebt intuitiv einen sogenannten Bra-Vektor \( \langle \phi | \) mit einem Ket-Vektor \( | \psi \rangle \) zusammen. Mathematisch exakt wäre der Bra-Vektor \( \langle \phi | \) dabei als sogenannte Linearform zu interpretieren, also als eine Abbildung, die angewendet auf einen Vektor eine komplexe Zahl liefert, wobei bestimmte Zusatzregeln gelten (siehe unten). Übrigens wird nun auch die Namensgebung (Bra- und Ket-Vektoren) klar: beide zusammen bilden eine braket, also eine Klammer (eben ein Skalarprodukt).
Das Skalarprodukt erfüllt nun wiederum eine Reihe von Axiomen (nur dann darf diese Abbildung auch so heißen):
Als Ansatz für den Zusammenhang zwischen Amplitude und Skalarprodukt wählen wir \[ A(\phi,\psi) = \langle \phi | \psi \rangle \] d.h. die Amplitude entspricht dem Skalarprodukt der Vektoren, die zu den physikalischen Zuständen gehören.
Damit ist unser mathematisches Modell komplett. Zustände werden durch Vektoren repräsentiert, und Amplituden durch Skalarprodukte zwischen diesen Vektoren.
Bleibt nun, zu überprüfen, ob dieses mathematische Modell alle Eigenschaften von Amplituden korrekt reproduziert. Weiter müssen wir überprüfen, wie der Zusammenhang zwischen quantenmechanischen Zuständen und Vektoren genauer aussieht: ist dieser Zusammenhang eindeutig? Und schließlich müssen wir die Frage nach der physikalischen Interpretation der mathematischen Ausdrücke stellen: ist jede Summe von Vektoren physikalisch interpretierbar, oder brauchen wir Zusatzregeln, die über die reinen Vektorraumaxiome hinausgehen?
Kommen wir zuerst zur zweiten Frage:
Betrachten wir dazu zwei Zustände \( | \psi \rangle \) und \( | \phi \rangle \). Wann sind diese Zustände gleich?
Nach unserer obigen Definition des Zustandes können wir sagen: wenn die vollständigen Messwertsätze gleiche Ergebnisse haben und sich auf die gleichen physikalischen Größen (z.B. Spin in z-Richtung) beziehen.
Es gibt aber noch eine zweite gleichwertige Möglichkeit, die Gleichheit von Zuständen zu definieren. Starten wir mit einem Zustand \( | \psi \rangle \) und fragen nach der Wahrscheinlichkeit, bei diesem Zustand für irgendwelche vollständigen Messgrößen den Messwertsatz zu messen, der dem Zustand \( | \phi \rangle \) entspricht.
Ein Beispiel: wir starten mit einem Zustand \( |\boldsymbol{p}, m_z \rangle \) (d.h. ein Fermion mit Impuls \(\boldsymbol{p}\) und Spinkomponente \(m_z\) in z-Richtung) und messen die Spinkomponente \(m_\alpha\) entlang einer Achse, die um den Winkel \(\alpha\) gegenüber der z-Achse geneigt ist. Den Impuls brauchen wir nicht weiter zu betrachten, denn er bleibt im Wesentlichen hier unberührt (die kleine Ablenkung im Magnetfeld wollen wir ja vernachlässigen).
Wie groß ist nun die Wahrscheinlichkeit, einen bestimmten Wert \(m_\alpha\) (z.B. \(m_\alpha = 1/2\) ) zu messen?
Diese Wahrscheinlichkeit ist gleich dem Betragsquadrat der zugehörigen Amplitude, also gleich \[ |A(m_\alpha, m_z)|^2 \] (den hier uninteressanten Impuls haben wir bei dieser Schreibweise wie oben auch einfach weggelassen). Nun gibt es aber zwei mögliche Messwerte für \(m_\alpha\), nämlich \(m_\alpha = 1/2\) und \(m_\alpha = -1/2\), und beide Messwerte treten auch auf. Daher ist die Wahrscheinlichkeit für jeden der beiden Messwerte normalerweise kleiner als 1. Nur für den Fall \( \alpha = 0 \) wissen wir schon vorher, welcher Messwert herauskommen wird, denn dann messen wir ja die Spinkomponente entlang der z-Achse, und deren Wert kennen wir ja bereits vor der Messung: es muss der vorgegebene Wert von \(m_z\) dabei herauskommen! Anders ausgedrückt: \[ |A(m_z, m_z)|^2 = 1 \] Das gilt auch ganz allgemein:
Das Betragsquadrat der Amplitude \(A(\phi,\psi)\) von zwei Zuständen \( | \psi \rangle \) und \( | \phi \rangle \) ist bei verschiedenen Zuständen kleiner als eins, da mehrere Messwerte möglich sind und das Betragsquadrat die Wahrscheinlichkeit für die jeweilige Möglichkeit darstellt. Nur wenn die beiden Zustände gleich sind, ist das Betragsquadrat der Amplitude gleich eins, denn dann ist es sicher, dass die entsprechende Messwertkombination auch gemessen wird. Es gilt also:
In unserem mathematischen Modell wollen wir die Amplitude durch das Skalarprodukt der beiden Zustandsvektoren \( | \psi \rangle \) und \( | \phi \rangle \) ausdrücken, also \[ A(\phi,\psi) = \langle \phi | \psi \rangle \] Sind die beiden Zustände gleich, so muss \[ |\langle \phi | \psi \rangle|^2 = 1 \] gelten. Was bedeutet das für die Vektoren \( | \psi \rangle \) und \( | \phi \rangle \), mit denen wir unsere Zustände ja mathematisch darstellen wollen? Ist diese mathematische Darstellung eindeutig?
Um diese Frage zu beantworten, geben wir einen Vektor \( | \psi \rangle \) vor und fragen, wie der Vektor \( | \phi \rangle \) aussehen kann, sodass \( |\langle \phi | \psi \rangle|^2 = 1 \) gilt.
Dazu zerlegen wir diesen Vektor in einen Anteil parallel zu \( | \psi \rangle \) und einen Anteil senkrecht zu \( | \psi \rangle \). Wir machen also den Ansatz \[ | \phi \rangle = a \, | \psi \rangle + | \rho \rangle \] mit \( \langle \rho | \psi \rangle = 0 \) (das meint man, wenn man von senkrechten Vektoren spricht). Eine solche Zerlegung ist bei Vektoren immer möglich. Wir setzen nun diesen Ansatz in unsere Gleichheitsbedingung für Zustände \( |\langle \phi | \psi \rangle|^2 = 1 \) ein und wenden die obigen Regeln für das Skalarprodukt an: \[ 1 = |\langle \phi | \psi \rangle|^2 = \] \[ = | a^* \, \langle \psi | \psi \rangle + \langle \rho | \psi \rangle |^2 = \] \[ = | a^* \, \langle \psi | \psi \rangle|^2 = |a|^2 \] denn \( \langle \rho | \psi \rangle = 0 \) und \( |\langle \psi | \psi \rangle|^2 = 1 \). Also muss \(a\) ist eine komplexe Zahl vom Betrag eins sein. Eine solche Zahl kann man auch schreiben als \[ a = e^{i \beta} \] mit einer reellen Zahl \(\beta\), die man auch die Phase von \(a\) nennt.
Nun muss andererseits auch \[ |\langle \phi | \phi \rangle|^2 = 1 \] gelten, denn wir haben es hier wieder mit zwei identischen Zuständen zu tun. Setzen wir den Ansatz wieder ein, so folgt \[ 1 = |\langle \phi | \phi \rangle|^2 = \] \[ = | a^* a \, \langle \psi | \psi \rangle + a^* \, \langle \psi | \rho \rangle + a \, \langle \rho | \psi \rangle + \langle \rho | \rho \rangle |^2 = \] \[ = | a^* a \, \langle \psi | \psi \rangle + \langle \rho | \rho \rangle |^2 = \] \[ = | 1 + \langle \rho | \rho \rangle |^2 \] und damit \[ \langle \rho | \rho \rangle = 0 \] Unsere Axiome für das Skalarprodukt sagen, dass diese Bedingung nur vom neutralen Element \( |0\rangle\) (dem Nullvektor) erfüllt wird (denn das Skalarprodukt sollte positiv definit sein), d.h. wir können diesen Vektor in unserem Ansatz \( | \phi \rangle = a \, | \psi \rangle + | \rho \rangle \) weglassen.
Mit \( a = e^{i \beta} \) lautet unser Ergebnis also:
Das ist eine erste kleine Überraschung, die man schnell übersehen kann! In unserem mathematischen Modell gibt es zu einem quantenmechanischen Zustand keinen eindeutigen Vektor, sondern alle Vektoren, die sich nur durch einen komplexen Zahlenfaktor vom Betrag eins unterscheiden, gehören zum gleichen Zustand. Mathematisch exakt müsste man daher sagen, dass ein Zustand durch eine sogenannte Äquivalenzklasse von Vektoren repräsentiert wird. Man spricht auch von einem sogenannten Strahl. Für konkrete quantenmechanische Berechnungen müssen wir natürlich einen dieser Vektoren auswählen, aber es darf für das Ergebnis (also für die berechneten Wahrscheinlichkeiten) keine Rolle spielen, welchen dieser Vektoren wir verwenden. Der Faktor \( e^{i \beta} \) darf im Ergebnis nicht vorkommen.
Wir sehen hier etwas, das in der Physik oft vorkommt: ein mathematisches Modell besitzt gewisse freie Parameter, die für das Ergebnis nicht relevant sind, die aber die Struktur des Modells mit bestimmen. Ein anderes Beispiel dafür sind die sogenannten Eichfreiheitsgrade in elektromagnetischen Potentialen (man kann beispielsweise zu einem elektrischen Potential eine Konstante hinzuaddieren, ohne dass sich das daraus berechnete elektrische Feld dadurch ändert).
Kümmern wir uns nun um die folgende Frage:
Die zentrale Formel für die Interferenz von Amplituden lautet (siehe oben) \[ A(\phi,\psi) = \sum_n A(\phi,n) \, A(n,\psi) \] In unserem mathematischen Modell muss daher gelten: \[ \langle \phi | \psi \rangle = \sum_n \, \langle \phi | n \rangle \, \langle n | \psi \rangle \] Tatsächlich gilt diese Formel allgemein für Vektorräume mit Skalarprodukt, wenn die Vektoren \( | n \rangle \) eine Orthonormalbasis des Vektorraumes bilden, denn dann kann man jeden Vektor \( | \psi \rangle \) als Linearkombination der Basisvektoren schreiben: \[ | \psi \rangle = \sum_n \, a_n \, | n \rangle \] Bilden wir das Skalarprodukt mit irgendeinem dieser Basisvektoren \( | m \rangle \) und verwenden, dass \[ \langle m | n \rangle = \delta_{m,n} \] ist (d.h. das Skalarprodukt zwischen identischen Basisvektoren ist Eins und zwischen verschiedenen Basisvektoren ist es Null; genau das ist ja eine Orthonormalbasis), so folgt \[ \langle m | \psi \rangle = \sum_n \, a_n \, \langle m | n \rangle = \] \[ = \sum_n \, a_n \, \delta_{m,n} = a_m \] und somit \[ | \psi \rangle = \sum_n \, | n \rangle \, \langle n | \psi \rangle \] Im Grunde ist es genau diese Formel, die den Vektorraum mit Skalarprodukt zu einem geeigneten mathematischen Modell der Quantentheorie werden lässt, denn damit reproduziert man automatisch die zentrale Formel für die Interferenz von Amplituden.
Übrigens kann man die obige Formel auch noch etwas anders auffassen: Man kann die Basisentwicklung eines Vektors \( | \psi \rangle \) nach orthonormalen Basisvektoren \( | n \rangle \) als Anwendung eines Operators auf den Vektor \( | \psi \rangle \) schreiben. Dieser Operator ist gleich dem Identitätsoperator (geschrienen als \(1\)), denn der Vektor wird ja nicht verändert. Es ist also \[ 1 = \sum_n \, | n \rangle \, \langle n | \] wobei \( \langle n | \) als lineare Abbildung zu sehen ist, die angewendet auf den Vektor \( | \psi \rangle \) das Skalarprodukt \( \langle n | \psi \rangle \) ergibt. Diese Schreibweise kann sehr nützlich sein, denn sie erlaubt es, in den Formeln an beliebiger Stelle eine geeignete Orthonormalbasis gleichsam einzuschieben.
Bleibt die Frage: Woher wissen wir, dass die Vektoren \( | n \rangle \) eine Orthonormalbasis des Vektorraumes bilden? Dass die Bedingung \( \langle m | n \rangle = \delta_{m,n} \) erfüllt werden kann, ist unmittelbar klar: die verschiedenen Möglichkeiten sind echte Alternativen, d.h. wenn eine Messwertkombination \( | n \rangle \) gemessen wird, kann keine andere Messwertkombination \( | m \rangle \) gemessen werden (das Fermion befindet sich beim Nachschauen entweder im oberen oder im unteren Teilstrahl).
Aber ist die Basis auch vollständig? Nun, das ist eine Forderung, die wir an den Vektorraum stellen müssen! Der für das betrachtete physikalische Problem geeignete Vektorraum muss die Menge aller Vektoren sein, die sich nach dieser Basis entwickeln lassen. Man sagt auch, er muss die lineare Hülle der Basis sein. Dabei müssen wir beachten, dass auch abzählbar unendlich viele Basisvektoren erlaubt sind, d.h. die Dimension des Vektorraums muss nicht endlich sein. In diesem Fall werden Konvergenzfragen zunehmend wichtig.
Wie steht es nun mit der Tatsache, dass mehrere Vektoren zum gleichen physikalischen Zustand gehören? Ein Faktor \( e^{i \beta} \) vor einem Zustandsvektor darf die Wahrscheinlichkeiten, die zu diesem Quantenzustand gehören, nicht ändern. Wie verträgt sich das mit der zentralen Formel \[ \langle \phi | \psi \rangle = \sum_n \, \langle \phi | n \rangle \, \langle n | \psi \rangle \] für die Interferenz von Amplituden?
Probieren wir es aus und multiplizieren in dieser Formel den Vektor \( | \psi \rangle \) mit diesem Faktor: \[ \langle \phi | e^{i \beta} \psi \rangle = \sum_n \, \langle \phi | n \rangle \, \langle n | e^{i \beta} \psi \rangle \] Zunächst einmal ist auch diese Formel mathematisch richtig, denn sie lässt sich aus der Formel ohne den Faktor durch Multiplikation mit \( e^{i \beta} \) herleiten. Sie muss aber andererseits genau dieselbe physikalische Situation beschreiben wie die ursprüngliche Formel ohne den Faktor, denn dieser darf keine Rolle spielen.
Betrachten wir zunächst die Amplitude auf der linken Seite. Die zugehörige Wahrscheinlichkeit ist gleich dem Betragsquadrat der Amplitude. Wegen \[ | \langle \phi | e^{i \beta} \psi \rangle |^2 = | e^{i \beta} \langle \phi | \psi \rangle |^2 = | \langle \phi | \psi \rangle |^2 \] spielt der Faktor für die Berechnung der Wahrscheinlichkeit keine Rolle. Analog auf der rechten Seite mit der Summe: Würden wir beobachten, welche der Möglichkeiten \( | n \rangle \) zutrifft (und dabei die Interferenz der Möglichkeiten zerstören), so spielt auch in dieser Wahrscheinlichkeit \[ | \langle n | e^{i \beta} \psi \rangle |^2 = | \langle n | \psi \rangle |^2 \] der Faktor keine Rolle.
Wichtig ist dabei, dass alle Amplituden, die den gleichen Zustand rechts enthalten, mit demselben Faktor \( e^{i \beta} \) multipliziert werden, denn dann ändert sich an der Interferenz dieser Amplituden nichts. Man sagt auch, dass Amplituden in diesem Sinne nur bis auf einen globalen Phasenfaktor eindeutig festgelegt sind. Relevant sind allein die Phasendifferenzen zwischen den interferierenden Amplituden. Genau diese Mehrdeutigkeit der Amplituden überträgt sich auf die Zustandsvektoren, die ebenfalls nur bis auf einen Phasenfaktor der Form \( e^{i \beta} \) festgelegt sind.
Vielleicht haben Sie sich über die Eigenschaft \[ a \, \langle \phi | \psi \rangle = \langle \phi | a \, \psi \rangle = \langle a^* \phi | \psi \rangle \] des Skalarproduktes gewundert (man sagt, das Skalarprodukt ist (sesqui-) linear bezüglich der Multiplikation mit den komplexen Zahlen). Aus der rechten Hälfte kann man also komplexe Zahlenfaktoren unverändert herausziehen. Beim Herausziehen aus der linken Hälfte muss man dagegen den Zahlenfaktor komplex konjugieren (Mathematiker definieren das übrigens oft genau anders herum).
Diese Eigenschaft ist notwendig, damit das Skalarprodukt positiv definit ist, d.h. \( \langle \psi | \psi \rangle \gt 0 \) wenn \( | \psi \rangle \) nicht das neutrale Element (also der Nullvektor \( | 0 \rangle \) ) ist. Nehmen wir an, wir könnten aus der linken Hälfte des Skalarproduktes Zahlenfaktoren unverändert herausziehen. Dann würde das Skalarprodukt des Vektors \( | \omega \rangle : = e^{i \beta} | \psi \rangle \) mit sich selbst folgendes ergeben: \[ \langle \omega | \omega \rangle = \langle e^{i \beta} \psi | e^{i \beta} \psi \rangle = e^{2 i \beta} \langle \psi | \psi \rangle \]
Für \( \beta = \pi/2 \) ist aber \( e^{2 i \beta} = e^{i \pi} = -1 \) damit wäre \( \langle \omega | \omega \rangle \lt 0 \) für \( \langle \psi | \psi \rangle \gt 0 \). Das Skalarprodukt wäre nicht mehr positiv definit für alle Vektoren.
Bleibt die Frage: muss das Skalarprodukt denn unbedingt positiv definit sein? Hätten wir auf die Forderung \( \langle \psi | \psi \rangle \gt 0 \) (wenn \( | \psi \rangle \) nicht der Nullvektor \( | 0 \rangle \) ist ) verzichten können?
Diese Frage ist gar nicht so leicht zu beantworten. Rein mathematisch wäre es durchaus denkbar, ohne diese Bedingung zu arbeiten. Man hätte dann kein Skalarprodukt, sondern eine sogenannte indefinite Metrik vor sich. Eine solche Metrik ist uns im Minkowskiraum (der Raumzeit) der speziellen Relativitätstheorie bereits begegnet. Dort gab es Vierervektoren \(v\), die die Bedingung \(g(v,v) = 0\) erfüllen, ohne gleich dem Nullvektor zu sein. Wir haben diese Vektoren als lichtartig bezeichnet.
Es zeigt sich aber, dass quantenphysikalische Theorien, die auf die Positivitätsbedingung verzichten, mit ernsthaften Schwierigkeiten zu kämpfen haben. Ein Beispiel für die Probleme, mit denen man zu kämpfen hat:
Wir hatten oben den Ansatz \[ | \phi \rangle = a \, | \psi \rangle + | \rho \rangle \] für alle Vektoren \( | \phi \rangle \) gemacht, die zum gleichen quantenmechanischen Zustand wie \( | \psi \rangle \) gehören. Um den Vektor \( | \rho \rangle \) loszuwerden, haben wir die Positivitätsbedingung des Skalarproduktes benötigt, d.h. ohne diese Bedingung würde ein Zustand durch eine viel größere Klasse von Vektoren repräsentiert. Eine Theorie mit einer solchen Struktur ist auf jeden Fall wesentlich komplexer als eine Theorie mit positiv definitem Skalarprodukt. Man muss im Detail untersuchen, ob die sich daraus ergebende mathematische Struktur auf die physikalischen Beobachtungen anwendbar ist. Fazit: ohne Zwang sollte man auf die Positivitätsbedingung schon aus praktischen Erwägungen nicht verzichten.
Die Tatsache, dass komplexe Zahlen aus der linken Seite des Skalarproduktes nur komplex konjugiert herausgezogen werden können, ist konsistent mit der Bedingung, dass das Skalarprodukt hermitesch ist: \[ \langle \psi | \phi \rangle = \langle \phi | \psi \rangle^* \] Das bedeutet, dass diese Beziehung auch für Wahrscheinlichkeitsamplituden gelten muss. Bisher sind wir aber auf diese Eigenschaft der Amplituden noch nicht gestoßen. Daher wollen wir nun zeigen, dass Amplituden sich tatsächlich so verhalten müssen. Dazu starten wir mit unserer allgemeinen Formel für die Interferenz von Amplituden \[ A(\phi,\psi) = \sum_n \, A(\phi,n) \, A(n,\psi) \] und setzen darin die beiden Zustände gleich: \[ A(\psi,\psi) = \sum_n \, A(\psi,n) \, A(n,\psi) \] Weiterhin wissen wir, dass \[ | A(\psi,\psi) |^2 = 1 \] ist, d.h. die Amplitude muss von der Form \( A(\psi,\psi) = e^{i \beta}\) sein. Zusammengefasst gilt also \[ \sum_n \, A(\psi,n) \, A(n,\psi) = e^{i \beta} \] Nun ist andererseits \( | A(n,\psi) |^2 \) die Wahrscheinlichkeit dafür, die Messwertkombination \( |n \rangle \) beim vorliegenden Zustand \( |\psi \rangle \) zu messen (wobei die Interferenz durch die Messung verloren geht). Da irgendeine dieser Messwertkombinationen \( |n \rangle \) mit Sicherheit gemessen wird (es gibt ja keine weitere Alternative), muss die Summe all dieser Wahrscheinlichkeiten gleich Eins sein: \[ \sum_n \, |A(n,\psi)|^2 = 1 \] Wir können diese Eins also rechts von \( e^{i \beta} \) in unserer vorherigen Formel heranmultiplizieren: \[ \sum_n \, A(\psi,n) \, A(n,\psi) = e^{i \beta} = \] \[ = e^{i \beta} \, \sum_n \, |A(n,\psi)|^2 \] Diese Formel sowie die Formel davor sollen für beliebige Zustände richtig sein. Man kann zeigen, dass für die einzelnen Summanden dann die Beziehung \[ A(\psi,n) \, A(n,\psi) = \] \[ = e^{i \beta} \, |A(n,\psi)|^2 = \] \[ = e^{i \beta} \, A(n,\psi)^* A(n,\psi) \] wobei wir \( |A(n,\psi)|^2 = A(n,\psi)^* A(n,\psi) \) verwendet haben. Die Amplitude \( A(n,\psi) \) kann man wegkürzen und erhält \[ A(\psi,n) = e^{i \beta} \, A(n,\psi)^* \] Wenn man die Zustände in der Amplitude vertauscht, so wird die Amplitude also komplex konjugiert. Zusätzlich kann mit einem willkürlicher Phasenfaktor multipliziert werden, der aber für alle interferierenden Amplituden gleich sein muss. Dies entspricht einfach nur der Tatsache, dass die Amplituden nur bis auf einen solchen gemeinsamen Phasenfaktor festgelegt sind. Die obige Formel wird durch die hermitesche Eigenschaft \( \langle \psi | n \rangle = \langle n | \psi \rangle^* \) des Skalarproduktes korrekt wiedergegeben.
Die Gleichung \( A(\psi,n) = e^{i \beta} \, A(n,\psi)^* \) bedeutet, dass die Wahrscheinlichkeit symmetrisch in den Zuständen ist: \[ |A(\psi,n)|^2 = |A(n,\psi)|^2 \] Das ist bemerkenswert! Die Wahrscheinlichkeit, bei einem Zustand \( | \psi \rangle \) die Messwertkombination \( | n \rangle \) zu messen, ist genauso groß wie die Wahrscheinlichkeit, bei einem Zustand \( | n \rangle \) die Messwertkombination \( | \psi \rangle \) zu messen! Das ist keineswegs selbstverständlich, sondern ist eine Folge davon, dass Amplituden zu verschiedenen Möglichkeiten miteinander interferieren, wenn die Möglichkeiten in diesem Experiment ununterscheidbar sind.
Wir sehen also, dass unser mathematisches Modell bisher alle Eigenschaften besitzt, die wir für die Beschreibung der Quantentheorie benötigen. Insbesondere konnten wir den Begriff des Zustandes in diesem Modell präzisieren und jedem Zustand eine Menge (einen Strahl) von Vektoren zuordnen. Mathematisch würde man sagen, dass die Abbildung der Zustände auf die Strahlen injektiv ist, d.h. zu jedem gegebenen Zustand gibt es einen eindeutigen Strahl von Vektoren.
Wie sieht es nun umgekehrt aus: Gibt es zu jedem Strahl von Vektoren auch einen quantenmechanischen Zustand?
Zunächst einmal gibt es eine ganz einfache Einschränkung: es muss \[ | \langle \psi | \psi \rangle |^2 = 1 \] gelten. Nicht alle Vektoren erfüllen diese Bedingung. Das ist jedoch keine besonders beeindruckende Einschränkung, denn aus jedem beliebigen Vektor \( | \psi' \rangle \) können wir einen passend normierten Vektor \[ | \psi \rangle := \frac{1}{\sqrt{\langle \psi' | \psi' \rangle}} \, | \psi' \rangle \] konstruieren, der die Bedingung erfüllt Anmerkung: Man kann auch auf die Normierungsbedingung verzichten und erst bei der Bildung der Wahrscheinlichkeiten geeignet normieren. Der Formalismus sieht dann etwas anders aus, aber die wesentliche Struktur ist identisch.
Eine andere Einschränkung aber ist viel wichtiger. Dazu stellen wir die Frage: Kann man beliebige Vektoren zu neuen Vektoren linearkombinieren, und entspricht dieser neue Vektor (normiert auf Eins) dann immer einem physikalischen Zustand? Können also beliebige Quantenzustände miteinander interferieren?
Betrachten wir dazu folgendes Beispiel: Gegeben sei ein Zustand \( | e \rangle \), der ein Elektron mit einem bestimmten Impuls und einer bestimmten Spinkomponente beschreibt. Weiter sei ein Zustand \( | p \rangle \) gegeben, der analog ein Proton beschreibt. Ist es möglich, diese beiden Zustände zu einem neuen quantenmechanischen Zustand (nennen wir ihn \( | N \rangle \) ) zu überlagern? \[ | N \rangle = a \, | e \rangle + b \, | p \rangle \] Die Antwort lautet ganz klar: Nein! Solche überlagerten Elektron-Proton-Zustände sehen wir in unserer Welt nicht.
Um zu verstehen, warum solche Überlagerungen keinen Sinn machen, schauen wir uns nochmal die allgemeine Formel für die Interferenz von Amplituden an. Sie lautete: \[ \langle \phi | \psi \rangle = \sum_n \, \langle \phi | n \rangle \, \langle n | \psi \rangle \] Hier interferieren die Amplituden zu verschiedenen ununterscheidbaren Alternativen \( | n \rangle \) miteinander (z.B. die beiden Teilstrahlen mit verschiedenem \(m_y\)). Anders ausgedrückt: Die dazu gleichwertige Addition \[ | \psi \rangle = \sum_n \, | n \rangle \, \langle n | \psi \rangle \] entspricht der Interferenz der verschiedenen ununterscheidbaren Möglichkeiten, die durch die Vektoren \( | n \rangle \) repräsentiert werden. Die Amplituden \( a_n = \langle n | \psi \rangle \) sind dabei die verschiedenen komplexen Gewichtsfaktoren (inklusive Phase), mit denen die Zustände \( | n \rangle \) aufsummiert werden müssen, um den Zustand \( | \psi \rangle \) zu ergeben.
Was würde dann der Ausdruck \[ | N \rangle = a \, | e \rangle + b \, | p \rangle \] physikalisch bedeuten? Man hätte ein Experiment vor sich, in dem zunächst ein quantenmechanischer Zustand \( | N \rangle \) für ein physikalisches Objekt (z.B. ein Teilchen) präpariert wird, der durch gewisse Messwerte gekennzeichnet ist. Die Messwerte von \( | N \rangle \) enthalten nicht die Information das Objekt ist ein Proton oder das Objekt ist ein Elektron, denn diese beiden Alternativen müssen ja ununterscheidbar sein, solange der Zustand \( | N \rangle \) für das Objekt besteht (sonst dürften wir sie nicht zum Zustand \( | N \rangle \) überlagern).
Nun stellen wir experimentell die Frage: Ist das Objekt ein Elektron oder ein Proton? Mit einer Wahrscheinlichkeit \(|a|^2\) finden wir dann im Experiment, dass das Objekt ein Elektron ist, und mit der Wahrscheinlichkeit \(|b|^2\) entpuppt es sich als Proton.
Nun haben Elektron und Proton unterschiedliche elektrische Ladungen, d.h. das physikalische Objekt, das durch den Zustand \( | N \rangle \) beschrieben wird, hat keinen definierten Wert für die Ladung – wir wissen ja noch nicht, ob im Experiment ein Elektron oder ein Proton erscheint, wenn wir eine entsprechende Messung an \( | N \rangle \) vornehmen.
Der Zustand \( | N \rangle \) ist aber auch keineswegs elektrisch neutral, denn dann würden die beiden Fragen Ist es ein Proton? und Ist es ein Elektron? beide eine negative Antwort erhalten, denn die Messung kann die Ladung nicht verändern (Ladungen sind in Summe immer erhalten).
Es zeigt sich nun, dass man Zustände, die keine definierte Ladung haben, experimentell nicht präparieren kann. Die elektrische Ladung eines Objektes ist eine Größe, die immer bekannt ist. Der Grund dafür ist, dass die elektrische Ladung mit einem elektrischen Feld verbunden ist, das weit in den Raum hinausreicht und das deshalb zwangsläufig irgendwelche Spuren in der Natur zurücklässt. Die beiden Alternativen Elektron oder Proton sind also immer unterscheidbar (auch wenn ich mich vielleicht für den Unterschied nicht interessiere).
Nun können Elektron und Proton gemeinsam bekanntlich ein Wasserstoffatom bilden. Kann man den Zustand \( | H \rangle \) des Wasserstoffatoms womöglich schreiben als \[ | H \rangle = a \, | e \rangle + b \, | p \rangle \] Auch dies geht nicht, denn ein Wasserstoffatom ist niemals gleich einem Elekron oder einem Proton, egal was man an ihm misst. Es enthält beides, aber es ist nicht die Interferenz der ununterscheidbaren Alternativen Elektron und Proton.
Stattdessen kann man beispielsweise die folgende Frage stellen: An welchen Orten \(\boldsymbol{x}_e\) und \(\boldsymbol{x}_p\) befinden sich Elektron und Proton im Wasserstoffatom, und wie ist deren jeweilige Spinkomponente \(m_{e,z}\) und \(m_{p,z}\) bezüglich der z-Achse? Die entsprechende Wahrscheinlichkeitsamplitude \[ \langle \boldsymbol{x}_e, m_{e,z}, \boldsymbol{x}_p, m_{p,z} | H \rangle \] ist eine sinnvolle physikalische Größe.
Die Tatsache, dass man nicht beliebig Zustände zu anderen Zuständen kombinieren kann, trägt den Namen Superauswahlregeln. Es existieren also Zusatzregeln, die nicht alle Linearkombinationen von Vektoren zulassen. Mit anderen Worten: Zu jedem Zustand gibt es einen Strahl von Vektoren, aber nicht zu jedem Strahl von Vektoren kann man auch einen physikalischen Zustand präparieren.
Es ist manchmal gar nicht so leicht, zu sehen, ob eine bestimmte Kombination zulässig ist oder nicht. Ist beispielsweise der Zustand \[ | N \rangle = a \, | \mathrm{Neutron} \rangle + b \, | \mathrm{Antineutron} \rangle \] sinnvoll? Sowohl Neutron als auch Antineutron sind ja elektrisch neutral. Man kann diese Frage nur beantworten, wenn man die physikalischen Randbedingungen kennt, unter denen man Zustände mit Neutronen oder Antineutronen experimentell erzeugen kann. In diesem Fall ist die Antwort: Man weiß immer, ob man ein Neutron oder ein Antineutron vor sich hat (Stichwort: Baryonenzahl), d.h. eine solche Superposition macht keinen Sinn.
Es gibt aber auch Beispiele, in denen ähnliche Superpositionen Sinn machen. Eines der berühmtesten Beispiele findet man bei Neutrinos. Etwas vereinfacht (Tau-Neutrinos werden ignoriert) passiert folgendes:
In der Sonne entstehen bei der Kernfusion sogenannte Elektron-Neutrinos \(\nu_e\), aber keine Myon-Neutrinos \(\nu_\mu\). Sonnennneutrinos werden also direkt nach ihrer Entstehung durch einen Vektor \( | \nu_e \rangle \) beschrieben. Die Eigenschaft, ob ein Elektron- oder ein Myon-Neutrino vorliegt, kann man messen, indem man das Neutrino mit Materie wechselwirken lässt. Ein Elektron-Neutrino kann sich dabei nur in ein Elektron verwandeln, aber niemals in ein Myon, und umgekehrt.
Nun kann man andererseits die Masse eines Neutrinos messen – zumindest im Prinzip, denn in der Praxis tun sich hier einige Probleme auf. Die Experimente zeigen, dass es (bei Weglassen der Tau-Neutrinos) zwei verschiedene mögliche Messwerte \(m_1\) und \(m_2\) für die Massen der Neutrinos gibt. Beide Massen sind sehr klein, aber größer als Null. Dabei ist die Neutrinomasse keine für jeden Neutrinozustand generell bekannte Größe, sondern es gibt bei einem Elektron-Neutrino eine große Wahrscheinlichkeit, die Masse \(m_1\) zu messen, aber auch eine gewisse kleine Wahrscheinlichkeit, die Masse \(m_2\) zu messen. Man kann also schreiben: \begin{align} | \nu_e \rangle &= a_1 \, | m_1 \rangle + a_2 \, | m_2 \rangle \\ & \\ | \nu_\mu \rangle &= b_1 \, | m_1 \rangle + b_2 \, | m_2 \rangle \end{align} Dabei ist der Betrag von \(a_1\) sehr viel größer als der von \(a_2\) und der Betrag von \(b_2\) sehr viel größer als der von \(b_1\). Daher bezeichnet man \(m_1\) auch oft als die Masse des Elektron-Neutrinos und \(m_2\) als die Masse des Myon-Neutrinos, obwohl das streng genommen nicht ganz korrekt ist, wenn \(a_2\) und \(b_1\) ungleich Null sind.
Wie verhalten sich nun diese Neutrino-Zustände im Lauf der Zeit? Erinnern wir uns, was wir in einem früheren Kapitel über die Zeitentwicklung von freien Teilchen-Zuständen mit definierter Masse gelernt haben: Ein Zustandsvektor, der zur Zeit Null gleich \( | m_1 \rangle \) ist, ist zu einem späteren Zeitpunkt \(t\) gleich \[ e^{- \frac{i}{\hbar} (E_1 t - \boldsymbol{p x})} \, | m_1 \rangle \] mit \[ E_1^2 = (m_1 c^2)^2 + (\boldsymbol{p} c)^2 \] (und analog für \( | m_2 \rangle \)).
Das führt dazu, dass zum Zeitpunkt \(t\) aus einem reinen Elektron-Neutrinozustand ein Zustand wird, der auch einen Anteil Myon-Neutrinozustand enthält. Es findet eine Art Schwebung statt, bei der periodisch die Wahrscheinlichkeit, ein Myon-Neutrino zu finden, von Null auf einen Maximalwert ansteigt und anschließend wieder auf Null abfällt. Man spricht von Neutrino-Oszillationen. In die Oszillationslänge geht dabei (in guter Näherung) der Term \(|m_1^2 - m_2^2|\) ein.
Anders als die elektrische Ladung ist zumindest bei Neutrinos deren winzige Masse nicht immer universell bekannt. Sie hinterlässt nicht automatisch immer erkennbare Spuren in unserer Welt. Deshalb ist sie auch so schwer zu messen, und deshalb gibt es bei Neutrinos auch Quanten-Superpositionen von Zuständen mit verschiedener Masse.
Kommen wir zu einem weiteren Punkt: Wie beschreibt man die Veränderung eines quantenmechanischen Zustandes, z.B. beim Durchgang durch irgendwelche Magnetfelder mit oder ohne Blockierung von Teilstrahlen? Dabei nehmen wir an, dass bei dieser Veränderung kein Informationsverlust eintritt, höchstens eine Informationsveränderung. Das System soll also weiterhin durch einen quantenmechanischen Zustand beschrieben werden, wenn auch evtl. durch einen anderen als vor der Veränderung. Beispielsweise kann der Zustand am Anfang durch die Spinkomponente \(m_z = 1/2\) gekennzeichnet sein, nach der Veränderung dagegen durch \(m_y = 1/2\).
Nennen wir den Zustand vor der Veränderung \( | \psi \rangle \) und nach der Veränderung \( | \phi \rangle \). Dann suchen wir eine Abbildung (nennen wir sie \(A\)), die aus \( | \psi \rangle \) den Vektor \( | \phi \rangle \) macht: \[ | \phi \rangle = A \, | \psi \rangle \] Der Operator \(A\) repräsentiert dann den Apparat bzw. den Mechanismus, der die Veränderung des Zustandes herbeiführt. Welche Eigenschaften muss \(A\) haben?
Wie immer, wenn es um die Eigenschaften neuer mathematischer Objekte geht, empfiehlt es sich, zu den Grundregeln für Amplituden zurückzukehren. Wir fragen also nach der Amplitude dafür, dass nach der Veränderung die Messwertkombination \( | \xi \rangle \) gemessen wird. Diese Amplitude ist gleich \[ \langle \xi | \phi \rangle = \langle \xi | A | \psi \rangle \] wobei der rechte Ausdruck das Skalarprodukt von \( | \xi \rangle \) mit dem Vektor \( A \, | \psi \rangle \) meint.
Nun kann das Ereignis, das zu dieser Amplitude gehört, folgendermaßen zerlegt werden: Es gibt verschiedene ununterscheidbare Möglichkeiten, wie die Veränderung eintreten kann. Mit der Amplitude \( \langle n | \psi \rangle \) haben wir den Zustand \( |n \rangle \) vor der Veränderung vorliegen. Nun gibt es eine Amplitude \(A_{mn}\), dass aus einem Zustand \( |n \rangle \) vor der Veränderung ein Zustand \( |m \rangle \) nach der Veränderung entsteht. Und schließlich gibt es eine Amplitude \( \langle \xi | m \rangle \), dass bei einem Zustand \( |m \rangle \) die Messwertkombination \( | \xi \rangle \) festgestellt wird.
Wir haben es hier mit der Interferenz von ununterscheidbaren Möglichkeiten zu tun, die jeweils durch zwei Messwertkombinationen \( |n \rangle \) und \( |m \rangle \) gekennzeichnet sind. Jede dieser Möglichkeiten wird dabei in drei Teilschritte zerlegt: Zustand \( |n \rangle \) wird gewählt, durch die Veränderung entsteht ein Zustand \( |m \rangle \), und schließlich wird die Messwertkombination \( | \xi \rangle \) gemessen. Nach unseren Regeln müssen wir die Amplituden der Teilschritte zu jeder Möglichkeit multiplizieren und dann über alle Möglichkeiten summieren: \[ \langle \xi | A | \psi \rangle = \sum_{m,n} \, \langle \xi | m \rangle \, A_{mn} \, \langle n | \psi \rangle \] Zur Veranschaulichung ein Beispiel: Wir beginnen mit einem Teilchenstrahl mit definiertem \(m_z\)-Wert, teilen den Strahl mit einem y-Magneten in zwei Strahlen mit verschiedenem \(m_y\)-Wert auf und führen diese Strahlen wieder zusammen, ohne zu überprüfen, in welchem Teilstrahl sich die Teilchen befinden. Das Aufteilen und wieder Zusammenführen bewirkt keine Veränderung am Zustand, verdeutlicht aber die beiden Möglichkeiten, die wir hier unterscheiden können. Nun schicken wir den Strahl durch den Apparat, der die Veränderung bewirkt, und teilen hinter dem Apparat den Strahl erneut in zwei \(m_y\)-Strahlen auf, die wir wieder zusammenführen. Zu guter Letzt messen wir \(m_\alpha\) entlang einer entsprechend gedrehten Achse. Eine der Möglichkeiten, die wir berücksichtigen müssen, wäre dann: Ein Teilchen mit \(m_z = 1/2\) wählt den Teilstrahl mit \(m_y = 1/2\), geht durch den Apparat, geht hinter dem Apparat durch den Teilstrahl mit \(m_y = - 1/2\), und am Schluss wird der Wert \(m_\alpha = 1/2\) gemessen.
Da die Formel oben für beliebige Vektoren \( | \xi \rangle \) gilt, können wir auch schreiben \[ A \, | \psi \rangle = \sum_{m,n} \, | m \rangle \, A_{mn} \, \langle n | \psi \rangle \] Mit Hilfe dieser Beziehung kann man leicht zeigen, dass A ein linearer Operator ist.
Und schließlich können wir weiter oben \( | \xi \rangle = |m' \rangle \) und \( | \psi \rangle = |n' \rangle \) wählen, wobei \( \langle m' | m \rangle = \delta_{m'm} \) und \( \langle n | n' \rangle = \delta_{nn'} \) sind. Es folgt \[ A_{mn} = \langle m | A | n \rangle \] Die Tatsache, dass alle Veränderungen von Zuständen durch die Wirkung linearer Operatoren auf den Zustandsvektoren beschrieben werden können, stellt eine große Vereinfachung dar. Um die Wirkung des Operators zu kennen, muss man nicht sämtliche Amplituden \( \langle \xi | A | \psi \rangle \) zwischen beliebigen Vektoren analysieren, sondern es genügen die Amplituden \( \langle m | A | n \rangle \) zwischen Orthonormalbasisvektoren.
Versuchen wir, herauszufinden, welche Sorte von Operatoren wir mit den möglichen Messwerten bei einer Messung in Verbindung bringen können. Dabei wollen wir weiterhin die Vereinfachung machen, dass nur diskrete (abzählbare) Messwerte möglich sind. Für kontinuierliche Messwerte wie den Impuls kann man sich dann vorstellen, dass man zunächst nur eine diskrete Menge von Werten betrachtet und dann diese Werte so dicht legt, dass die gewünschte Genauigkeit erreicht wird. Eine mathematische Präzisierung für kontinuierliche Messwerte werden wir später kennen lernen.
Betrachten wir ein physikalisches System, das durch den quantenmechanischen Zustandsvektor \( | \psi \rangle \) beschrieben wird (d.h. ein entsprechender vollständiger Satz von Messgrößen ist bekannt). Mit Hilfe einer geeigneten Apparatur führen wir nun die Messung einer physikalischen Größe (beispielsweise die Spinkomponente entlang der z-Achse) durch. Wenn wir sehr viele solcher Messungen an vielen identischen Systemen durchführen, so werden wir feststellen, dass bestimmte Messwerte (nennen wir sie \( \lambda_n \)) mit gewissen Wahrscheinlichkeiten \(P_n\) auftreten. Die entsprechenden Wahrscheinlichkeitsamplituden lauten \( \langle n | \psi \rangle \), d.h. \[ P_n = | \langle n | \psi \rangle |^2 \] Nach der Messung befindet sich das System im Zustand \(|n\rangle\), der zum gefundenen Messwert \(\lambda_n\) gehört. Das bedeutet: Ein vollständiger Satz von Messwerten muss bekannt sein, in dem der Messwert \(\lambda_n\) vorkommt.
Wir wollen nun einen Operator suchen, der den zu erwartenden Mittelwert (Erwartungswert) der Messwerte für den gegebenen Zustand \( | \psi \rangle \) ausdrückt, wobei die Messwerte mit ihrer auftretenden Wahrscheinlichkeit gewichtet werden. Nennen wir diesen Erwartungswert \( \langle \lambda \rangle_\psi \), d.h. \[ \langle \lambda \rangle_\psi = \sum_n \, P_n \, \lambda_n \] Wir können nun \(P_n = | \langle n | \psi \rangle |^2 = \langle \psi | n \rangle \, \langle n | \psi \rangle \) verwenden und erhalten \[ \langle \lambda \rangle_\psi = \sum_n \, \langle \psi | n \rangle \, \lambda_n \, \langle n | \psi \rangle \] Damit haben wir den gesuchten Operator gefunden: er lautet \[ A := \sum_n \, | n \rangle \, \lambda_n \, \langle n | \] Dabei sind die \(\lambda_n\) reelle Zahlen, denn sie sind ja die Messwerte. Die Formel bedeutet, dass die Wirkung von \(A\) auf jeden beliebigen Zustandsvektor \( |\psi \rangle \) gegeben ist durch \[ A \, |\psi \rangle = \sum_n \, | n \rangle \, \lambda_n \, \langle n |\psi \rangle \] Mit Hilfe von \(A\) können wir den Mittelwert schreiben als \[ \langle \lambda \rangle_\psi = \langle \psi | A |\psi \rangle \] Der Operator \(A\) hat nun einige interessante Eigenschaften:
Es gilt sogar umgekehrt (etwas vereinfacht), dass hermitesche Operatoren generell reelle Eigenwerte haben, und dass die zugehörigen (auf 1 normierten) Eigenvektoren eine Orthonormalbasis bilden (für den Beweis sei auf die Standardlehrbücher der linearen Algebra verwiesen), d.h. jeder hermitesche Operator (mit diskreten Eigenwerten) lässt sich schreiben als \( A = \sum_n \, | n \rangle \, \lambda_n \, \langle n | \) .
Im Fall von unendlich vielen Eigenwerten muss man allerdings dabei noch einige Konvergenzbedingungen stellen, und im Fall von kontinuierlichen Eigenwerten geht die Summe in ein Integral über (wir kommen noch darauf zurück). Details findet man in Büchern zur Funktionalanalysis. Wie so oft in der Physik ignorieren wir zunächst solche mathematischen Feinheiten und kümmern uns erst darum, wenn sie wichtig werden.
Zum Abschluss dieses recht umfangreichen und sicher nicht ganz einfachen Kapitels wollen wir noch einmal zum Begriff des Zustandes zurückkommen und uns fragen, was passiert, wenn wir ein quantenmechanisches System nicht durch einen Zustand beschreiben können.
Im Grunde ist ein quantenmechanischer Zustand der Idealfall in der Quantentheorie. Er bedeutet, dass wir eine vollständige, nicht erweiterbare Information über das physikalische System besitzen.
Für ein einzelnes Elektron bedeutet das beispielsweise, dass wir seinen Impuls \(\boldsymbol{p}\) und seine Spinkomponente \(m_z\) bezüglich der z-Achse kennen. Sein Zustand wird dann durch den Vektor \( |\boldsymbol{p}, m_z \rangle \) beschrieben (den Impuls wollen wir diesmal nicht weglassen).
Wenn wir nun die Spinkomonente entlang einer Achse messen, die um den Winkel \( \alpha \) gegenüber der z-Achse geneigt ist, so ist die Wahrscheinlichkeit für das Auftreten eines bestimmten Wertes von \(m_\alpha\) gegeben durch das Betragsquadrat der Amplitude \( \langle \boldsymbol{p}, m_\alpha | \boldsymbol{p}, m_z \rangle \), und der Erwartungswert für die Spinkomponente \( m_\alpha \) ist gegeben durch \[ \langle m_\alpha \rangle_{\boldsymbol{p}, m_z} = \] \[ = \sum_{m_\alpha} \, |\langle \boldsymbol{p}, m_\alpha | \boldsymbol{p}, m_z \rangle|^2 \, m_\alpha = \] \[ = \sum_{m_\alpha} \, \langle \boldsymbol{p}, m_z | \boldsymbol{p}, m_\alpha \rangle \, m_\alpha \, \langle \boldsymbol{p}, m_\alpha | \boldsymbol{p}, m_z \rangle = \] \[ =: \sum_{m_\alpha} \, \langle \boldsymbol{p}, m_z | A \, | \boldsymbol{p}, m_z \rangle = \] mit \[ A := \sum_{m_\alpha} \, | \boldsymbol{p}, m_\alpha \rangle \, m_\alpha \, \langle \boldsymbol{p}, m_\alpha | \] Die Summe geht dabei über die beiden Werte \(m_\alpha = \pm 1/2 \). Der Impuls soll bei der Messung nicht verändert werden.
Wie aber sollen wir vorgehen, wenn bei unserem zu messenden Zustand lediglich der Impuls, nicht aber der Wert der Spinkomponente \(m_z\) bekannt ist? Das ist beispielsweise der Fall, wenn wir eine Elektronenquelle vor uns haben, die einen unpolarisierten oder nur teilweise polarisierten Elektronenstrahl (mit konstantem Impuls) ausstößt.
Wenn wir die Spinkomponente \(m_z\) messen, so werden wir mit einer gewissen Wahrscheinlichkeit \(P_{+1/2}\) den Wert \(m_z = +1/2 \) und mit einer gewissen Wahrscheinlichkeit \(P_{-1/2}\) den Wert \(m_z = -1/2 \) finden. Nun könnte der Elektronenstrahl möglicherweise durch irgendeinen Zustand \( |\boldsymbol{p}, m_\beta \rangle \) beschrieben werden, so dass \(P_{m_z} = | \langle \boldsymbol{p}, m_z | \boldsymbol{p}, m_\beta \rangle|^2 \) ist. Ob das so ist, wissen wir beispielsweise, wenn wir \(m_\beta\) messen. Kommt hier immer derselbe Wert heraus, liegt ein reiner Zustand vor.
Im Allgemeinen aber wird die Elektronenquelle keinen solchen reinen Zustand aussenden, sondern ein statistisches Gemisch von \(m_z\)-Werten. In diesem Fall verhält sich der Strahl oft so, als hätten wir zwei unabhängig voneinander entstandene Strahlen mit \(m_z = +1/2\) bzw. \(m_z = -1/2\) gemischt. Dabei treten im Experiment nun zwei unterscheidbare Alternativen auf: Das Teilchen stammt aus dem einen oder dem anderen Strahl.
Wir können nun nach der Wahrscheinlichkeit fragen, bei diesem gemischten Strahl den Messwert \(m_\alpha\), also einen bestimmten Spinwert entlang einer geneigten Achse, zu messen. Diese Wahrscheinlichkeit ist die Summe der Wahrscheinlichkeiten der einzelnen Möglichkeiten (\(m_z\)-Werte), wobei die Warscheinlichkeit jeder dieser Möglichkeiten sich zusammensetzt aus der Wahrscheinlichkeit \( |\langle \boldsymbol{p}, m_\alpha | \boldsymbol{p}, m_z \rangle|^2 \), beim Zustand \( | \boldsymbol{p}, m_z \rangle \) den Wert \( m_\alpha \) zu messen, mal der Wahrscheinlichkeit \(P_{m_z}\), mit der dieser Zustand im statistischen Gemisch der \(m_z\)-Werte beiträgt: \[ P_{m_\alpha} = \sum_{m_z} \, P_{m_z} \, |\langle \boldsymbol{p}, m_\alpha | \boldsymbol{p}, m_z \rangle|^2 \] Nochmal zur Erinnerung: hier werden nicht Amplituden, sondern Wahrscheinlichkeiten addiert! Es gibt keine Interferenz der Möglichkeiten.
Analog zur Vorgehensweise beim hermiteschen Operator \(A\) oben können wir diesen Ausdruck auch schreiben als \[ P_{m_\alpha} = \langle \boldsymbol{p}, m_\alpha | \, \rho \, | \boldsymbol{p}, m_\alpha \rangle \] mit dem Operator \[ \rho := \sum_{m_z} \, | \boldsymbol{p}, m_z \rangle \, P_{m_z} \, \langle \boldsymbol{p}, m_z | \] Dieser Operator wird auch als Dichteoperator oder als statistischer Operator bezeichnet. Er beschreibt ein allgemeines quantenmechanisches Objekt inclusive derjenigen, die nicht durch einen reinen Zustand beschrieben werden können.
Auch für einen Strahl, der sich in einem reinen Zustand \( |\boldsymbol{p},m_\beta \rangle \) befindet, ist diese Schreibweise anwendbar, denn dann ist einfach \(P_{m_\beta} = 1 \) für diesen Wert von \(m_\beta\) (und Null für alle anderen), d.h. \[ \rho = | \boldsymbol{p}, m_\beta \rangle \, \langle \boldsymbol{p}, m_\beta | \] Die allgemeine Form des Dichteoperators lautet \[ \rho = \sum_{\xi} \, | \xi \rangle \, P_\xi \, \langle \xi | \] mit geeigneten Zuständen \( | \xi \rangle \), bezüglich derer man die Wahrscheinlichkeiten \( P_\xi \) kennt. Die Zustände \( | \xi \rangle \) müssen dabei nicht unbedingt orthogonal zueinander sein (man könnte ja beispielsweise zwei Teilchenstrahlen überlagern, die jeweils durch einen Zustand \( | m_\alpha \rangle \) bzw. \( | m_\beta \rangle \) charakterisiert werden, wobei sich die Winkel \(\alpha\) und \(\beta\) nicht exakt um 90 Grad unterscheiden).
Wir hatten oben gesehen, dass wir bei einem reinen Zustand \( | \psi \rangle \) den Erwartungswert einer Messgröße mit möglichen Messwerten \(\lambda_n\) schreiben können als \[ \langle \lambda \rangle_\psi = \langle \psi | A | \psi \rangle \] wobei der hermitesche Operator \[ A := \sum_n \, | n \rangle \, \lambda_n \, \langle n | \] die Messgröße charakterisiert. Wie lässt sich dieses Ergebnis auf ein System verallgemeinern, das nicht durch einen reinen Zustand charakterisiert werden kann, sondern durch ein statistisches Gemisch von Zuständen beschrieben werden muss, also durch einen Dichteoperator \(\rho\)?
Zunächst einmal ist der Erwartungswert immer gegeben durch \[ \langle \lambda \rangle_\psi = \sum_n \, P_n \, \lambda_n \] Dabei ist \(P_n\) die Wahrscheinlichkeit dafür, den Messwert \(\lambda_n\) zu messen. Nach unserem obigen Ergebnis ist bei einem statistischen Gemisch von Zuständen diese Wahrscheinlichkeit gegeben durch \[ P_n = \langle n | \rho | n \rangle \] d.h. es ist \[ \langle \lambda \rangle_\psi = \sum_n \, \langle n | \rho | n \rangle \, \lambda_n \] In diesem Ausdruck können wir nun eine beliebige vollständige Orthonormalbasis \[ 1 = \sum_j \, | j \rangle \, \langle j | \] vor dem Operator \(\rho\) einschieben und erhalten \begin{align} \langle \lambda \rangle_\psi &= \sum_{n, j} \, \langle n | j \rangle \, \langle j | \rho | n \rangle \, \lambda_n = \\ & \\ &= \sum_{n, j} \, \langle j | \rho | n \rangle \, \lambda_n \, \langle n | j \rangle = \\ & \\ &= \sum_{j} \, \langle j | \rho \, A | j \rangle \end{align} mit \[ A = \sum_n \, | n \rangle \, \lambda_n \, \langle n | \] Man bezeichnet den Ausdruck rechts auch als die Spur des Operatorprodukts \( \rho \, A \). Dabei ist egal, mit welcher Orthonormalbasis \( |j\rangle\) die Spur berechnet wird, denn die Spur ist unabhängig von der Wahl dieser Basis. Unser Ergebnis lautet also: \[ \langle \lambda \rangle_\psi = \sum_{j} \, \langle j | \rho \, A | j \rangle = \mathrm{Spur} (\rho \, A) \] Betrachten wir noch einmal den Unterschied zwischen reinen Zuständen und einem statistischen Gemisch aus Zuständen aus einem etwas anderen Blickwinkel. Bei einem reinen Zustand \( |\psi\rangle\) war der Dichteoperator gegeben durch \( \rho = | \psi \rangle \, \langle \psi | \). Wir können nun vor und hinter diesem Operator eine vollständige Orthonormalbasis \( |n\rangle \) bzw. \( |m\rangle \) einschieben: \[ \rho = | \psi \rangle \, \langle \psi | = \] \[ = \sum_{m,n} \, |m\rangle \, \langle m | \psi \rangle \, \langle \psi |n\rangle \, \langle n | = \] \[ = \sum_{m,n} \, |m\rangle \, \rho_{mn} \, \langle n | \] mit \[ \rho_{mn} = \langle m | \psi \rangle \, \langle \psi |n\rangle \] Man bezeichnet \(\rho_{mn}\) auch als Dichtematrix. Wir können uns nun vorstellen, dass aufgrund irgendeines physikalischen Vorgangs (z.B. unkontrollierter Kontakt mit der Umgebung) der reine Zustand \( |\psi\rangle\) zerstört wird und langsam in ein statistisches Gemisch übergeht. Dabei werden typischerweise die Nicht-Diagonalelemente der Dichtematrix immer kleiner, so dass die Dichtematrix beispielsweise in einzelne Diagonalblöcke zerfällt.
Im Extremfall bleiben nur noch die Diagonalelemente zurück, d.h. \[ \rho_{mn} = P_n \, \delta_{mn} \] Dann wird die Dichtematrix zu \[ \rho = \sum_{n} \, |n\rangle \, P_n \, \langle n | \] d.h. übrig bleibt ein statistisches Gemisch von einzelnen Zuständen \( |n\rangle \). Das Verschwinden von Nicht-Diagonalelementen der Dichtematrix ist also gleichbedeutend mit dem Übergang von reinen Zuständen zu statistischen Zustandsgemischen. Man spricht auch von Dekohärenz.
Fassen wir den Inhalt dieses Kapitels noch einmal zusammen:
Wir haben ein mathematisches Modell gefunden, das die Regeln zum Rechnen mit Wahrscheinlichkeitsamplituden widerspiegelt und das hilft, die entsprechenden Rechnungen klar und übersichtlich zu strukturieren. Dabei haben wir nichts Neues hinzuerfunden, sondern nur bereits bekanntes Wissen in anderer Form dargestellt. Ganz zentral war dabei, dass Amplituden als Interferenz ununterscheidbarer Alternativen geschrieben werden können.
Als geeignetes mathematisches Modell hat sich der sogenannte Hilbertraum erwiesen, also ein vollständiger komplexer Vektorraum mit einem hermiteschen, positiv definitem Skalarprodukt und einer abzählbaren Basis. Quantenmechanische Zustände entsprechen dabei Strahlen in diesem Hilbertraum (also Mengen von normierten Vektoren, die sich nur durch einen komplexen Phasenfaktor unterscheiden), und Amplituden entsprechen dem Skalarprodukt zwischen den Vektoren.
Dabei haben wir mögliche Probleme, die mit unendlichen Summen oder kontinuierlichen Messwerten zusammenhängen, zunächst einfach ignoriert. Weitere Probleme werden in der relativistischen Quantentheorie auf uns zukommen (Stichwort Renormierung). Wir haben also in diesem Kapitel den groben Rahmen kennengelernt, wie er jeder Quantentheorie zugrunde liegt. Nun gilt es, die Details auszuarbeiten: Wie sehen die Vektorräume im Detail aus? Wie verändern sich Zustände mit der Zeit? Wie wirken sich Symmetrietransformationen (z.B. Drehungen) aus? Welche Messwerte sind möglich? Wie sehen vollständige Messwertsätze aus, und welche Messungen sind miteinander verträglich?
Diesen und weiteren Fragen wollen wir uns in den nun folgenden Kapiteln zuwenden.
© Jörg Resag, www.joerg-resag.de
last modified on 19 July 2023