Zusammenfassung des Buchkapitels:
Ist die Quantenmechanik eine unvollständige Theorie? Verfügen Teilchen über innere Eigenschaften (verborgene Variablen), die ihr Verhalten festlegen, auch wenn diese Eigenschaften für die Quantenmechanik oder auch für uns unsichtbar sind? Im Buchkapitel wird versucht, dieser Frage anhand einer typisch quantenmechanischen Erscheinung auf den Grund zu gehen: dem Spin!
Wie weit lässt sich der Spin durch einen klassischen Drehimpuls darstellen (siehe folgende Grafik)?

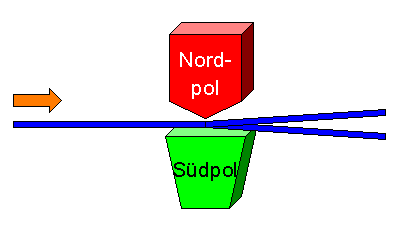
Schickt man einen Strahl neutraler Spin-1/2-Teilchen (z.B. Silberatome)
durch ein senkrechtes inhomogenes Magnetfeld,
so werden die Teilchen immer um einen festen Winkel
nach oben oder nach unten abgelenkt, so dass sich der Strahl in zwei Teilstrahlen aufteilt.
Daraus kann man schließen,
dass die Spinkomponente \(M\) parallel zu einer beliebig vorgegebenen
Richtung immer entweder +1/2 oder -1/2 ist.
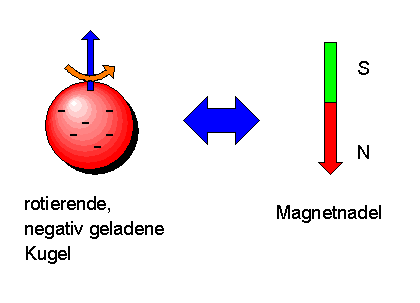
Unser klassisches Bild des Spins als rotierende Kugel
bzw. Magnetnadel gerät dadurch in erste Schwierigkeiten, da die Rotationsachse
beliebige Winkel zum Magnetfeld besitzen kann, so dass ein Kontinuum von Ablenkwinkeln
zu erwarten wäre. Man kann aber mit geeigneten Zusatzannahmen immer noch versuchen,
eine klassische Erklärung mithilfe rotierender Kugeln dafür zu finden (siehe Buchkapitel).
Stellen wir hinter dem Magneten für den nach oben abgelenkten Strahl einen weiteren Magneten auf, dessen Magnetfeld um neunzig Grad gekippt ist, so beobachten wir, dass bei den zuvor nach oben abgelenkten Teilchen jeweils die Hälfte durch den zweiten Magneten um einen bestimmten Winkel nach rechts oder nach links abgelenkt wird:
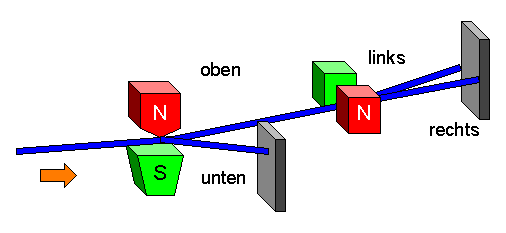
Auch dieses Versuchsergebnis lässt sich mit Hilfe geeigneter Zusatzannahmen
noch durch rotierende Kugeln erklären (siehe Buch).
Ist also der Teilchenspin vielleicht doch durch einen klassischen Drehimpuls
(also durch eine lokale innere Teilcheneigenschaft) erklärbar?
Erst im Jahre 1964 konnte diese Frage durch den damals am CERN bei Genf arbeitenden jungen englischen Physiker John Stewart Bell weitgehend geklärt werden. Die Kernidee lässt sich mit dem folgenden Versuchsaufbau erklären (Stichwort Einstein-Rosen-Podolsky-Paradoxon):
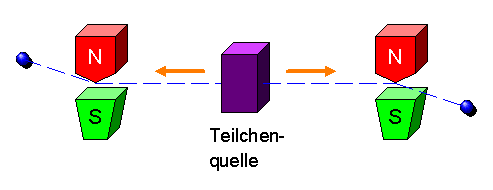
Jedesmal, wenn eines der beiden Teilchen in diesem Versuch nach oben abgelenkt wird,
so wird das andere Teilchen nach unten abgelenkt und umgekehrt.
Das können wir zunächst problemlos durch entgegengesetzt rotierende Kugeln erklären.
Ohne eine solche lokale innere Teilcheneigenschaft, die das Verhalten festlegt (nämlich die Teilchenrotation) müssten sich die Teilchen beim Erreichen der Magneten absprechen, was bei großen Entfernungen Überlichtgeschwindigkeit erfordert, im Widerspruch zu Einsteins spezieller Relativitätstheorie. Man scheint also auf lokale innere Teilcheneigenschaften hier nicht verzichten zu können, d.h. die Quantenmechanik wäre unvollständig.
Bell kam nun auf die Idee, die Orientierung der Magnetfelder einzeln zu verdrehen:
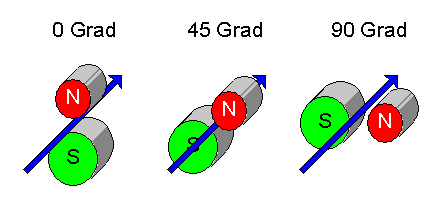
Dabei bringen wir hinter den beiden
Magneten eine Abschirmung an,
die den zum Südpol abgelenkten Strahl absorbiert, so dass nur der
in Richtung Nordpol abgelenkte Teilstrahl den Magneten passieren
kann.
Falls es verborgene Teilcheneigenschaften gibt, die im Voraus bereits festlegen, wie sich ein Teilchen beim Durchgang durch ein Magnetfeld verhält, so lassen sich diese Teilchen anhand dieser Eigenschaften in verschiedene Gruppen aufteilen, wobei ein Teilchen gleichzeitig zu mehreren Gruppen gehören kann – die Gruppen können also überlappen.
Für die Rotationsachsen ergibt sich damit folgendes Bild (Details siehe Buchkapitel):
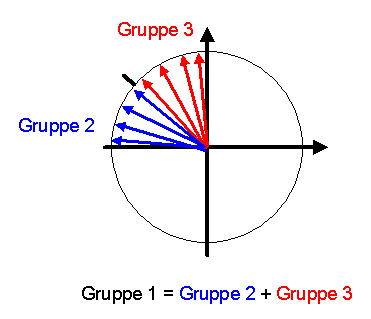
Jedes Teilchen der ersten Gruppe gehört, falls es auch bei 45 Grad
durchkommt, außerdem zur dritten Gruppe, oder andernfalls zur zweiten Gruppe.
Die Gruppen 2 und 3 umfassen zusammen also alle Teilchen der
Gruppe 1 und sind damit zusammen genommen mindestens
so groß wie diese Gruppe.
Für Teilchenpaare, die sich immer entgegengesetzt zueinander verhalten, erwarten wir entsprechend:
+
Die Wahrscheinlichkeit dafür, dass bei einem Teilchenpaar das erste Teilchen bei 45 Grad und das Partnerteilchen bei 90 Grad durchkommt (Gruppe 3)
≥
Die Wahrscheinlichkeit dafür, dass bei einem Teilchenpaar das erste Teilchen bei 0 Grad und das Partnerteilchen bei 90 Grad durchkommt (Gruppe 1)
Diese Ungleichung trägt den Namen Bellsche Ungleichung. Sie gilt unausweichlich, falls die Teilchen über lokale innere Eigenschaften verfügen, die ihr Verhalten im Magnetfeld physikalisch eindeutig bestimmen, unabhängig davon, ob wir in der Lage sind, diese Eigenschaften alle vollständig zu messen.
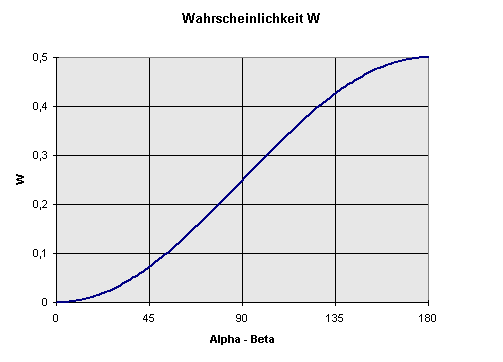
Die Quantenmechanik sagt zu diesen Wahrscheinlichkeiten folgendes: Die Wahrscheinlichkeit \(W\) dafür, dass ein Teilchen einen um den Winkel \(\alpha\) gedrehten Magneten passiert und sein Partnerteilchen den gegenüberliegenden, um den Winkel \(\beta\) gedrehten Magneten ebenfalls passiert, ist gegeben durch die Formel (Herleitung siehe Zusatzinfos unten) \[ W = \frac{1}{2} \, \left( \sin{ \frac{\alpha - \beta}{2} } \right)^2 \]
Die Wahrscheinlichkeit dafür, dass
ein Teilchen einen um den Winkel \(\alpha\) gedrehten Magneten
passiert und sein Partnerteilchen den gegenüberliegenden, um den
Winkel \(\beta\) gedrehten Magneten ebenfalls passiert.
Berechnen wir nach dieser Formel nun die Wahrscheinlichkeit \(W\)
für die verschiedenen Werte der Verdrehungswinkel
der beiden Magneten, so erhalten wir das folgende Ergebnis:
Für Gruppe 2 mit \( \alpha = 0 \) Grad und \( \beta = 45 \) Grad ergibt sich die Wahrscheinlichkeit \(W\) zu etwa 0,0732, ebenso für Gruppe 3 (\(\alpha = 45\) Grad und \(\beta = 90\) Grad), während die Wahrscheinlichkeit für Gruppe 1 (\(\alpha = 0\) Grad und \(\beta = 90\) Grad) genau 0,25 ist.
Die Wahrscheinlichkeit für Gruppe 2 und Gruppe 3 zusammen beträgt aber nur \(2 \cdot 0,0732 = 0,1464\) und liegt damit deutlich unter der geforderten Mindestmarke von 0,25. Die Quantenmechanik verletzt die Bellsche Ungleichung!
Die experimentellen Ergebnisse stimmen vollständig mit dem Ergebnis der quantenmechanischen Berechnung überein. Daraus müssen wir entnehmen, dass die Quantenmechanik und mit ihr die Natur selbst eine Erklärung des Spins durch lokale innere Eigenschaften der Teilchen (z.B. dessen Rotationsachse) ausschließt. Ein Teilchen hat in der Quantenmechanik keine Rotationsachse! Die Quantenmechanik scheint in diesem Sinne keine Unvollständigkeiten aufzuweisen. Die Angabe von Wahrscheinlichkeiten ist nach allem, was wir heute wissen, die einzige Möglichkeit, die physikalischen Gesetze der Natur zu formulieren. Auch moderne Experimente bestätigen das immer wieder.
Wenn es aber den Spin (und auch andere Messgrößen wie Ort und Impuls) nicht als lokale innere Eigenschaften von Teilchen gibt, wie schaffen es die beiden Teilchen oben dann, sich auf weite Entfernungen hin abzustimmen? Müssen sie nicht Informationen mit Überlichtgeschwindigkeit austauschen?
Zumindest kann man das korrelierte Verhalten der Teilchenpaare nicht nutzen, um Informationen mit Überlichtgeschwindigkeit zu versenden, denn die Korrelation ist nur sichtbar, wenn man das Verhalten beider Teilchen kennt. Immerhin lässt sich dieses Verhalten aber zur abhörsicheren Verschlüsselung nutzen (mehr dazu in Die Grenzen der Berechenbarkeit, Kapitel 5.9 Kryptographie – die Kunst der Verschlüsselung).
Dennoch bleibt das abgestimmte Verhalten der Teilchenpaare rätselhaft. Der Ausweg aus diesem Dilemma besteht darin, sowohl auf innere Eigenschaften als auch auf eine lokale Beschreibung der Teilchen zu verzichten. Die Quantenmechanik beschreitet genau diesen Weg! Sie macht nur eine Aussage über die Wahrscheinlichkeiten für das gemeinsame Verhalten beider Teilchen:
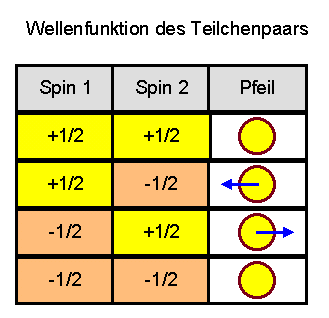
Niels Bohr hat gesagt, dass es unterhalb
einer gewissen klassischen, makroskopischen Stufe keine
Realität im gewohnten Sinne mehr gibt.
Es sieht so aus, als hätte er Recht gehabt.
a) Herleitung der Formel für W
b) Spin, Kreisströme und magnetisches Dipolmoment, g-Faktor
In den Zusatzinfos zu Kapitel 2.7 wurden die beiden Amplituden für die Spinausrichtung in und gegen eine vorgegebene Raumachse (z-Achse) dargestellt. Sie lauten (wir schreiben hier vereinfacht \( c_{+} \) statt \( c_{+ 1/2} \) etc.): \[ c_{+} = \cos{ \left( \frac{\theta}{2} \right) } \, e^{ i \frac{\varphi}{2}} \] \[ c_{-} = \sin{ \left( \frac{\theta}{2} \right) } \, e^{- i \frac{\varphi}{2}} \] Dabei sind \(\theta\) und \(\varphi\) reelle Zahlen (Drehwinkel). Diese Parametrisierung ist zunächst ganz allgemein, denn zwei komplexe Zahlen, deren Betragsquadrate zusammen Eins ergeben müssen und bei denen es nur auf den relativen Drehwinkel \(\varphi\) zueinander ankommt, lassen sich immer so schreiben.
Nun ist \( |c_{+}|^{2} \) die Wahrscheinlichkeit dafür, dass der Spin in Richtung der z-Achse gemessen wird, und analog \( |c_{-}|^{2} \) für die Gegenrichtung. Dadurch erhalten die Winkel \(\theta\) und \(\varphi\) eine physikalische Interpretation, denn bei \(\theta = 0\) zeigt der Spin garantiert in Richtung der z-Achse und bei \(\theta = \pi\) (Bogenmaß) garantiert gegen die z-Richtung.
Eine genaue Analyse von Drehungen in der Quantentheorie zeigt, dass man \(\theta\) und \(\varphi\) als Drehwinkel interpretieren kann: Wenn man einen Spin, der zunächst in z-Richtung zeigt, um den Winkel \(\theta\) gegen die z-Richtung kippt und dann mit dem Winkel \(\varphi\) um die z-Richtung dreht, so geben die obigen Formeln danach genau die z-Wahrscheinlichkeitsamplituden für die Messwahrscheinlichkeiten bezüglich der alten z-Achse an. In Kapitel 2.7 hatten wir dies durch die Bloch-Kugel dargestellt.
Wie sehen die Amplituden für einen Spin aus, der zunächst gegen die z-Richtung zeigt und ebenfalls um einen Winkel \(\theta\) gegen die z-Achse gekippt wird? Ganz einfach: Wir fangen wieder mit einem Spin in z-Richtung an, kippen diesen aber diesmal um den Winkel \( \theta + \pi \) gegen die z-Achse (wobei \(\pi\) im Bogenmaß gleich 180 Grad ist). Der Spin wird also erst um 180 Grad und dann um den Winkel \(\theta\) gekippt. Die entsprechenden Amplituden für Messungen entlang der z-Achse lauten: \[ d_{+} = \cos{ \left( \frac{\theta + \pi}{2} \right) } \, e^{ i \frac{\varphi}{2}} = \] \[ = - \sin{ \left( \frac{\theta}{2} \right) } \, e^{ i \frac{\varphi}{2}} \] \[ d_{-} = \sin { \left( \frac{\theta + \pi}{2} \right) } \, e^{ - i \frac{\varphi}{2}} = \] \[ = \cos{ \left( \frac{\theta}{2} \right) } \, e^{ - i \frac{\varphi}{2}} \] Man kann die Interpretation nun im Sinne unseres Experimentes etwas abwandeln: Statt den Spin um den Winkel \(\theta\) gegen die z-Achse zu kippen und dann die unveränderte z-Achse als Messachse für die Spinkomponente zu verwenden, kann man alternativ auch den Spin unverändert lassen und die Messachse um den Winkel \(- \theta\) kippen. Die obigen Amplituden beziehen sich dann auf Spinmessungen entlang der gekippten Achse bei einem Spin, der unverändert in oder gegen die z-Richtung zeigt.
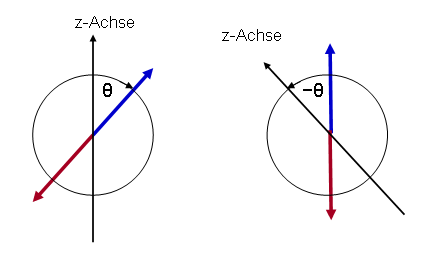
Rechts: Dieselbe Situation anders interpretiert: Blauer und roter Spin zeigen in Richtung der alten z-Achse,
aber die neue z-Achse wurde um den Winkel \(- \theta\) gekippt.
Die Wahrscheinlichkeitsamplituden für die Spinmessung entlang der neuen z-Achse
sind \(c_{+}\) und \(c_{-}\) für den blauen Spin und
\(d_{+}\) und \(d_{-}\) für den roten Spin.
Nun zu unserem Experiment mit den beiden Teilchen, die immer entgegengesetzten Spin aufweisen,
wenn man für beide Teilchen dieselbe Messachse verwendet.
Den ersten Magneten hatten wir um den Winkel \(\alpha\) und den zweiten Magneten um den Winkel \(\beta\)
gegen die z-Achse gekippt, wobei die Kippbewegung senkrecht zur Flugbahn der Teilchen erfolgt.
Wir legen nun zunächst die z-Achse neu fest: Sie soll in Richtung des Nordpols
des ersten Magneten zeigen, so dass dieser Magnet bezogen auf die neue z-Achse
nicht mehr gekippt ist.
Der zweite Magnet ist gegenüber der neuen z-Achse also um den Winkel \( \beta - \alpha \) gekippt. Diesen Winkel wollen wir \( - \theta \) nennen: \[ - \theta := \beta - \alpha \] Der zweite Magnet ist also um den Winkel \( - \theta \) gegen die neue z-Achse gekippt, misst also die Spinkomponente des zweiten Teilchens entlang dieser gekippten Richtung, während der erste Magnet die Spinkomponente des ersten Teilchens entlang der ungekippten neuen z-Achse misst.
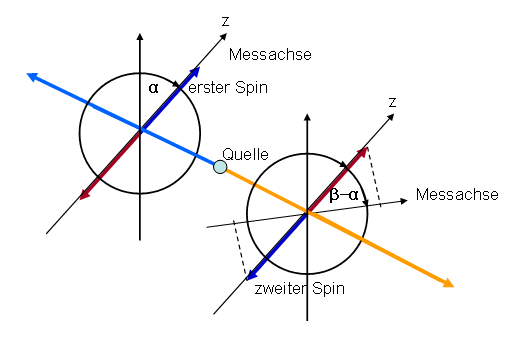
Die entsprechenden Wahrscheinlichkeitsamplituden wollen wir
\[
a_{++} , \, a_{+-} , \, a_{-+} , \, a_{--}
\]
nennen, d.h. \( a_{++} \) ist die Wahrscheinlichkeitsamplitude dafür, dass
am ersten Magneten der Teilchenspin parallel zur neuen z-Richtung gemessen wird und zugleich
am zweiten Magneten der dortige Teilchenspin parallel zur dortigen Messachse gemessen wird.
Schauen wir uns die beiden Amplituden \( a_{++} \) und \( a_{+-} \) an. Bei ihnen ist der Spin am ersten Magneten bekannt: er zeigt in die neue z-Richtung (dunkelblauer Pfeil links oben in der Grafik). Also muss der zweite Spin entgegen der neuen z-Richtung zeigen (dunkelblauer Pfeil rechts unten in der Grafik). Diesen zweiten Spin messen wir nun im zweiten Magneten in einer Richtung, die um den Winkel \( - \theta \) gegen die neue z-Achse gekippt ist. Genau diesen Fall hatten wir oben bereits betrachtet und durch die beiden d-Amplituden beschrieben. Es muss also gelten (wobei wir noch einen Normierungsfaktor \( \frac{1}{\sqrt{2}} \) zufügen, so dass die Summe aller Amplituden-Längenquadrate gleich 1 wird): \[ a_{++} = \frac{1}{\sqrt{2}} d_{+} = - \frac{1}{\sqrt{2}} \, \sin{ \left( \frac{\theta}{2} \right) } \, e^{ i \frac{\varphi}{2}} \] \[ a_{+-} = \frac{1}{\sqrt{2}} d_{-} = \frac{1}{\sqrt{2}} \, \cos{ \left( \frac{\theta}{2} \right) } \, e^{ - i \frac{\varphi}{2}} \] Analog zeigt bei den beiden Amplituden \( a_{-+} \) und \( a_{--} \) der erste Spin gegen die neue z-Richtung, der zweite Spin also in die neue z-Richtung (dunkelrotes Pfeilpaar in der Grafik), so dass die Messung des zweiten Spins in der gekippten Richtung die folgenden Amplituden ergibt: \[ a_{-+} = \frac{1}{\sqrt{2}} c_{+} = \frac{1}{\sqrt{2}} \, \cos{ \left( \frac{\theta}{2} \right) } \, e^{ i \frac{\varphi}{2}} \] \[ a_{--} = \frac{1}{\sqrt{2}} c_{-} = \frac{1}{\sqrt{2}} \, \sin{ \left( \frac{\theta}{2} \right) } \, e^{- i \frac{\varphi}{2}} \] Nun können wir die gewünschten Wahrscheinlichkeiten leicht ablesen. So ist die Wahrscheinlichkeit \(W\) dafür, dass der Spin am ersten Magnet in Richtung der neuen z-Achse zeigt und der Spin am zweiten Magneten in Richtung der dortigen Messachse zeigt, gegeben durch:
| \[ W = |a_{++}|^{2} = \frac{1}{2} \, \left[ \sin{ \left( \frac{\theta}{2} \right) } \right]^2 = \] \[ = \frac{1}{2} \, \left[ \sin{ \left( \frac{\alpha - \beta}{2} \right) } \right]^2 \] |
Das ist genau die im Buchkapitel sowie oben angegebene Formel.
Im Buchkapitel (siehe auch oben) haben wir uns das Verhalten eines elektrisch neutralen Teilchens mit Spin 1/2 durch eine rotierende außen negativ geladene elektrische Kugel veranschaulicht und gesagt, dass sich diese Kugel wie eine kleine Magnetnadel verhält, was die magnetischen Kräfte auf sie betrifft. Etwas allgemeiner kann man auch sagen: Ein Teilchen mit Spin 1/2 besitzt ein magnetisches Dipolmoment (auch magnetisches Moment, Dipolmoment oder kurz Dipol genannt) ähnlich desjenigen, wie es eine rotierende geladene Kugel, also letztlich ein kleiner Kreisstrom besitzt.
Machen wir uns zunächst klar, wie das Magnetfeld eines Kreisstroms in einem kleinen kreisförmigen Draht aussieht (die rotierende Kugel entspricht dann mehreren übereinander gestapelten Kreisströmen mit unterschiedlichem Radius):
Von den Maxwellgleichungen her wissen wir, dass die Magnetfeldlinien einen geraden stromführenden Leiter nach der rechten-Hand-Regel umfließen, wobei der Daumen die Stromrichtung und die gekrümmten Finger die Richtung des Magnetfeldes angeben.
Nun biegen wir den Draht zu einem Kreis, so dass der Strom von oben gesehen gegen den Uhrzeigersinn fließt. Die Magnetfeldlinien fließen nun von unten nach oben durch diesen Kreis hindurch und laufen außen in weitem Bogen wieder nach unten zurück. Ganz ähnlich laufen auch in einer kleinen Magnetnadel in ihrem Inneren die Magnetfeldlinien vom Südpol zum Nordpol, treten dort aus der Magnetnadel hervor und laufen außen in weitem Bogen wieder zum Südpol zurück. In etwas größerer Entfernung sieht das Magnetfeld des Kreisstroms daher praktisch genauso aus wie das Magnetfeld der kleinen Magnetnadel, deren Nordpol nach oben zeigt. Man spricht daher dort auch einfach vom Feld eines magnetischen Dipols.
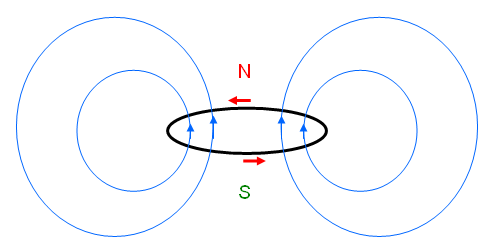
Das Magnetfeld einer stromführenden Kreißchleife.
Der Strom (rote Pfeile) fließt von oben gesehen gegen den Uhrzeigersinn.
Die Magnetfeldlinien durchstoßen die Kreisfläche von unten nach oben
und laufen außen in einem Bogen nach unten zurück.
In größerer Entfernung sieht das Magnetfeld aus wie das einer Magnetnadel,
deren Nordpol nach oben zeigt. Entsprechend wurde auch für die Magnetschleife
ein Nord- und ein Südpol eingezeichnet (N und S), d.h. das magnetische Dipolmoment zeigt nach oben.
Ähnlich sieht auch das Magnetfeld einer geladenen rotierenden Kugel aus,
die man sich aus mehreren Kreisströmen zusammengesetzt vorstellen kann.
Bei der im Buchkapitel abgebildeten negativ geladenen Kugel (siehe auch die Zusammenfassung oben)
fließt der Strom formal übrigens genau anders
herum, da sich dort negative Ladungen bewegen (die Stromrichtung
bezieht sich immer auf bewegte
positive Ladungen, so dass sich negative Ladungen entgegen der formalen
Stromrichtung bewegen) – daher liegt dort der
Nordpol der entsprechenden Magnetnadel unten.
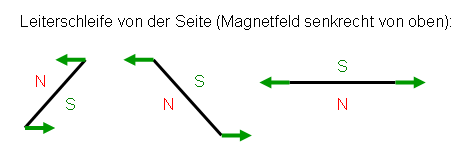
Die magnetischen Kräfte auf einen kleinen Kreisstrom in einem von außen vorgegebenen Magnetfeld kann man anschaulich am Besten verstehen, wenn man statt der kreisförmigen eine rechteckige Leiterschleife betrachtet (wobei die physikalischen Effekte in beiden Fällen letztlich dieselben sind). Das äußere Magnetfeld soll dabei wie im Buchkapitel senkrecht von oben nach unten verlaufen und die Leiterschleife kann gekippt sein, so dass zwei ihrer vier Seiten schräg zum Magnetfeld verlaufen, während die beiden anderen Seiten horizontal und damit senkrecht zum Magnetfeld liegen. Den Strom lassen wir wie zuvor zunächst wieder gegen den Uhrzeigersin umlaufen (von oben gesehen).
Aus den Zusatzinfos zu Kapitel 1.4 (Maxwellgleichungen) wissen wir, dass ein Stromfluss in jedem Teilstück der Leiterschleife zu einer Kraft führt, die senkrecht zum Stromfluss und senkrecht zum vorgegebenen Magnetfeld wirkt. Dabei gilt wieder eine Rechte-Hand-Regel (UVW-Regel): Der Daumen entspricht der Stromrichtung (Ursache U), der Zeigefinger entspricht dem Magnetfeld (Vermittler V) und die Kraft entspricht dem Mittelfinger (Wirkung W). Damit ergibt sich, dass die Kraft auf jede der vier Seiten der Leiterschleife im Bild unten horizontal nach Innen wirkt. Dabei heben sich die Kräfte der beiden gekippten Seitenstücke gegenseitig auf, während die Kräfte der beiden horizontalen Seiten zu einem Drehmoment führen, denn eine der beiden Seiten liegt weiter oben als die andere.
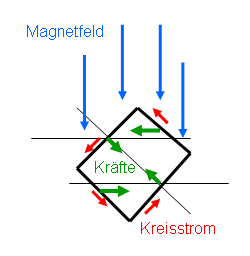
Die Kräfte der beiden horizontalen Seitenstücke
versuchen, die Leiterschleife solange weiter zu kippen, bis beide Kräfte
horizontal nach außen zeigen und kein weiteres Drehmoment mehr ausüben, sondern
nur noch erfolglos versuchen, die Leiterschleife horizontal auseinanderzuziehen.
Die Leiterschleife läge dann horizontal mit einem Stromfluss im Uhrzeigersinn
(von oben gesehen) und entspräche einer Magnetnadel mit dem Nordpol unten und dem
Südpol oben. Das entspricht unserer Anschauung, dass sich gleiche Magnetpole
abstoßen, so dass es den Nordpol der Magnetnadel zum unten liegenden
Südpol des äußeren Magnetfeldes zieht.
Für die rotierende außen negativ geladene Kugel im Buchkapitel bedeutet das analog, dass
das äußere Magnetfeld deren Rotationsachse senkrecht nach oben kippen will,
so dass sie von oben gesehen links herum rotiert (siehe die erste Abbildung in
der Kapitelzusammenfassung). Da aber die Kugel einen Drehimpuls aufweist,
lässt sie sich nicht einfach kippen,
sondern wird sich wie ein Kreisel bewegen, d.h. die Rotationsachse wird
eine Präzessionsbewegung um die Magnetfeldlinien ausführen.
Dabei bleibt der Winkel zwischen Rotationsachse (Dipolmoment)
und Magnetfeld praktisch konstant:

Quelle:
Wikimedia Commons File:Gyroscope precession.gif von Lucas Vieira, dort gemeinfrei.
Damit wäre das Drehmoment auf die rotierende Kugel soweit klar.
Bleibt noch zu klären, was geschieht, wenn das Magnetfeld zum Nordpol hin (also nach oben)
stärker wird, so wie es beim Stern-Gerlach-Versuch der Fall ist.
Da alle Kräfte auf die Leiterschleife senkrecht zum Magnetfeld und damit
in horizontaler Richtung wirken, kann es scheinbar trotzdem
keine Kraft nach oben oder unten geben.
Doch Vorsicht: Wenn das Magnetfeld nach oben hin stärker werden soll, so kann es nicht vollkommen senkrecht verlaufen, denn die Magnetfeldlinien müssen nach oben hin dichter werden. Daher kann man sich vorstellen, dass die Magnetfeldlinien an den beiden horizontalen Seiten der Leiterschleife leicht schräg liegen, so dass sie nach oben hin langsam zusammenlaufen. Die Kräfte auf diese Seitenstücke müssen weiterhin senkrecht zum Magnetfeld liegen. Sie zeigen daher entweder nach innen und dabei leicht schräg nach unten, oder nach außen und dabei leicht schräg nach oben. Im ersten Fall läuft der Strom von oben gesehen gegen den Uhrzeigersinn, d.h. der Nordpol liegt weiter oben, und es wirkt insgesamt eine Kraft nach unten auf die Leiterschleife. Der Nordpol wird gleichsam stärker nach unten gedrückt als der Südpol nach oben, da er weiter oben liegt und das Magnetfeld dort stärker ist. Im zweiten Fall ist es genau umgekehrt.
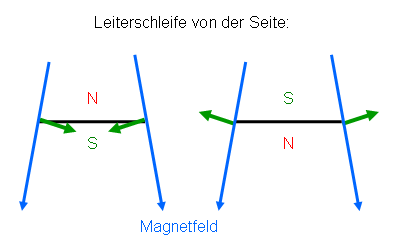
Die Kraft im inhomogenen Magnetfeld ist umso stärker, je
paralleler das Dipolmoment zum Magnetfeld liegt.
Wenn wir bei den geladenen rotierenden Kugeln von zufällig ausgerichteten Rotationsachsen
und damit Dipolmomenten ausgehen, so sollten alle möglichen Kräfte und damit Ablenkungen
nach oben und unten vorkommen, da ja die Rotationsachse ihren Winkel mit dem Magnetfeld
bei der Präzessionsbewegung beibehält. Im realen Stern-Gerlach-Versuch mit neutralen
Spin-1/2-Teilchen findet man dagegen nur zwei Ablenkungen, so als ob die
Rotationsachse (der Spin) und damit das magnetische Dipolmoment nur
nach oben oder nach unten zeigen könnte. Mehr dazu im Buchkapitel.
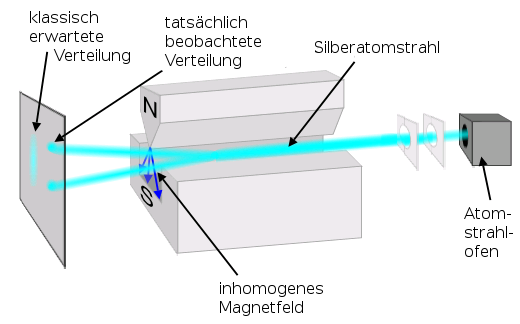
Stern-Gerlach-Versuch.
Der Nordpol des Magneten wurde als scharfe Kante ausgeprägt, um die notwendige
Inhomogenität des Magnetfeldes zu erreichen.
Credit: Theresa Knott,
Quelle:
Wikimedia Commons File:Stern-Gerlach Experiment de.png,
CC BY-SA 3.0 DEED
Hier noch einige Formeln, die die obigen Zusammenhänge präzisieren:
Das magnetische Dipolmoment bezeichnen wir dabei durch einen Vektor \( \boldsymbol{\mu} \) (oft wird auch die Bezeichnung \(\boldsymbol{m}\) verwendet, aber das wird zu leicht mit der Masse verwechselt). Er zeigt bei einer Magnetnadel von deren Südpol zum Nordpol. Bei der Leiterschleife kann man sich die Richtung des Dipolmoments wieder mit einer Rechten-Hand-Regel merken: Die gekrümmten Finger zeigen in Richtung des Stroms und das Dipolmoment in Richtung des ausgestreckten Daumens, also bei der oben abgebildeten Kreißchleife nach oben. Bei einer ebenen beliebig geformten Leiterschleife gilt für den Betrag von \(\boldsymbol{\mu}\) die Formel \[ |\boldsymbol{\mu}| = I \, A \] Dabei ist \( I \) der umlaufende Strom und \( A \) die von der Leiterschleife umlaufende Fläche (siehe z.B. Wikipedia: Magnetisches Moment). Bei der rotierenden geladenen Kugel ist die Formel etwas komplizierter.
Die auf die Schleife wirkende Drehkraft drückt man durch das sogenannte Drehmoment \( \boldsymbol{N} \) aus. Dabei ist ( \boldsymbol{N} \) ein Vektor, der in Richtung der Drehachse zeigt und bei dem die Drehkraft von seiner Spitze aus gesehen gegen den Uhrzeigersinn wirkt. Im Magnetfeld \( \boldsymbol{B} \) wirkt auf das magnetische Moment \( \boldsymbol{\mu} \) das Drehmoment \[ \boldsymbol{N} = \boldsymbol{\mu} \times \boldsymbol{B} \] wobei \( \times \) das Vektor-Kreuzprodukt steht.
Man kann diese Formel für das Drehmoment am Beispiel der Rechteckschleife auch leicht herleiten – wir verzichten hier darauf. Im Bild oben mit den drei von der Seite gezeigten schrägstehenden Leiterschleifen zeigt das Dipolmoment in den ersten zwei Ausrichtungen nach links oben bzw. links unten, das Magnetfeld nach unten und daher das Drehmoment aus der Zeichenebene auf den Betrachter, so dass die Drehkraft gegen den Uhrzeigersinn wirkt. In der dritten Ausrichtung zeigt das Dipolmoment nach unten und ist damit parallel zum Magnetfeld, so dass die Drehkraft Null wird.
In einem inhomogenen statischen Magnetfeld (mit \( \mathrm{rot} \, \boldsymbol{B} = 0 \)) wirkt zusätzlich zum Drehmoment die Kraft \[ \boldsymbol{F} = (\boldsymbol{\mu} \, \mathrm{grad}) \, \boldsymbol{B} = \] \[ = \mathrm{grad} \, ( \boldsymbol{\mu} \boldsymbol{B} ) \] In unserem obigen Beispiel ist das Skalarprodukt \( \boldsymbol{\mu} \boldsymbol{B} \) positv, wenn der Dipol nach unten in Magnetfeldrichtung zeigt, und wird nach oben hin größer, da \( |\boldsymbol{B}| \) zunimmt, so dass der Gradient und damit die Kraft nach oben wirken. Zeigt der Dipol nach oben, wirkt die Kraft dagegen nach unten. Liegt der Dipol horizontal, so wirkt gar keine Kraft, da das Skalarprodukt Null wird.
Man kann einen interessanten Zusammenhang zwischen magnetischem Dipolmoment und Drehimpuls herleiten, wenn man annimmt, dass die in einem Kreisstrom im Abstand \(r\) umlaufenden Ladungen zugleich eine bestimmte Masse tragen. Der umlaufende Kreisstrom \( I \) ist gleich der insgesamt umlaufenden Gesamtladung \( q \), dividiert durch die Umlaufzeit \[ T = \frac{2 \pi r}{v} \] also \[ I = \frac{q}{T} = \frac{q v}{2 \pi r} \] wobei \(v\) die Geschwindigkeit der (positiven) Ladungen und damit der Massen ist. Damit haben wir \[ \mu := |\boldsymbol{\mu}| = I \, A = \] \[ = \frac{q v}{2 \pi r} \, \pi r^{2} = q v \frac{r}{2} = q \, \frac{L}{2m} \] wobei wir den nichtrelativistischen Drehimpuls \[ L = r m v \] verwendet haben. Dabei ist \( m \) die insgesamt zusammen mit der Ladung umlaufende Masse, so wie \(q\) die insgesamt umlaufende Ladung ist. Wenn die umlaufenden Ladungen positiv sind, so sind die Vektoren \(\boldsymbol{\mu}\) und \(\boldsymbol{L}\) parallel ausgerichtet, andernfalls antiparallel, was man durch das Vorzeichen von \(q\) ausdrücken kann, so dass gilt: \[ \boldsymbol{\mu} = \frac{q}{2m} \, \boldsymbol{L} \] Bei komplizierteren Ladungs- und Massenverteilungen tritt noch ein zusätzlicher Zahlenfaktor auf, der von der genauen Form der Verteilungen abhängt. Er wird g-Faktor (gyromagnetischer Faktor, Landé-Faktor) genannt: \[ \boldsymbol{\mu} = g \, \frac{q}{2m} \, \boldsymbol{L} \] Diese Formel gilt auch für Teilchen mit Spin, obwohl der Spin eigentlich nur quantenmechanisch verstanden werden kann und daher nur teilweise einem klassischen Drehimpuls entspricht.
Man kann den g-Faktor des Elektrons und Myons im Rahmen der Quantenfeldtheorie des Standardmodells sehr genau berechnen, und man kann ihn zugleich auch sehr genau messen. Bereits die einfache relativistische Diracgleichung ergibt für punktförmige Fermionen einen sehr guten Schätzwert, nämlich \[ g = 2 \] (die Herleitung findet man beispielsweise in Wikipedia: Dirac-Gleichung).
Die Einbeziehung der Polarisationswolke im Rahmen der Quantenfeldtheorie des Standardmodells vergrößert diesen Wert noch um etwa ein Tausendstel, so dass er schließlich sehr genau mit dem experimentellen Messwert übereinstimmt, wobei man beim Myon allerdings eine winzige, aber signifikante Abweichung findet, die man als Hinweis auf eine Physik jenseits des Standardmodells deutet. Weitere Details zum g-Faktor des Elektrons und Myons findet man in Buchkapitel 5.1.
Wie misst man den g-Faktor eigentlich? Wie wir von oben wissen, kann man dazu entweder die Ablenkung in einem inhomogenen Magnetfeld oder das Drehmoment in einem homogenen Magnetfeld messen. Schauen wir uns die zweite Möglichkeit genauer an:
Von oben wissen wir: Das Drehmoment in einem homogenen Magnetfeld führt bei schrägstehendem Spin (Dipolmoment) zu einer Präzessionsbewegung der Rotationsachse um die magnetischen Feldlinien, ähnlich wie bei einem Kreisel. Auch quantenmechanisch stimmt das, wenn man die Spinorientierung dort durch passende Spinamplituden ausdrückt (siehe die Zusatzinfos zu Kapitel 2.7 sowie oben die Herleitung für \(W\)).
Die entsprechende Umlauffrequenz der Drehachse bezeichnet man auch als Larmorfrequenz. Sie ist proportional zum g-Faktor sowie zur Magnetfeldstärke. Diese Larmorfrequenz kann man nun messen. Bei Myonen (und Antimyonen) ist auf diese Weise bis zum Jahr 2004 am Brookhaven National Laboratory der g-Faktor mit großer Präzision bestimmt worden (siehe The E821 Muon (g-2) Home Page, zu neueren Messungen siehe auch Wikipedia: Muon g-2). Schauen wir uns an, wie das gelungen ist:
Um Myonen zu erzeugen, werden zunächst in einem Beschleuniger Protonen auf hohe Energien gebracht. Diese Protonen lässt man nun mit Materie kollidieren, wobei u.a. viele negativ geladenen Pionen entstehen, die wiederum jeweils in ein Myon und ein Myon-Antineutriono zerfallen. Da beim Myon-Antineutrino der Spin immer in die Flugrichtung orientiert ist und da die Pionen spinlos sind, muss auch der Spin der Myonen in Flugrichtung zeigen (Stichwort Paritätsverletzung, siehe die Zusatzinfos zu Kapitel 6.1).
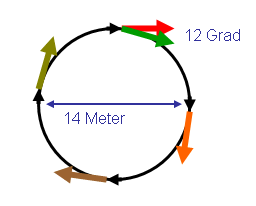
Die so erzeugten hochenergetischen Myonen (Energie etwa 3 GeV) mit Spins in Flugrichtung füllt man nun in einen sogenannten Speicherring (Durchmesser etwa 14 Meter), in dem ein senkrechtes homogenes Magnetfeld herrscht, so dass die Myonen in diesem Ring horizontal fast mit Lichtgeschwindigkeit kreisen. Die entsprechende Umlauffrequenz nennt man auch Zyklotronfrequenz. Zugleich führt die Spinachse des Myons eine Präzessionsbewegung aus, kreist also mit der Larmorfrequenz um die senkrechten Magnetfeldlinien.
Wäre nun der g-Faktor exakt zwei, wie es die Diracgleichung angibt, so wären beide Frequenzen exakt gleich groß. Die Spinachse würde sich genauso schnell verändern wie die Bewegungsrichtung des Myons, und zwar in dieselbe Drehrichtung, so dass der Spin immer in Bewegungsrichtung zeigen würde.
Da aber die virtuellen Teilchen der Myon-Polarisationswolke zu einer Vergrößerung des g-Faktors um etwa ein Promille führen, dreht sich die Spinachse etwas schneller als die Bewegungsrichtung, und zwar pro Umlauf um etwa 12 Grad, so dass nach etwa 29 Umläufen im Ring sich die Spinachse einmal mehr gedreht hat, also 30 Mal.
Daraus lässt sich direkt die Abweichung des g-Faktors vom Wert 2 ablesen, was eine extrem hohen Messgenauigkeit für den g-Faktor ergibt. Das Experiment enthält mit der Umlauffrequenz (Zyklotronfrequenz) direkt einen passenden Vergleichswert für die Larmorfrequenz, und der Unterschied dieser zwei Frequenzen ergibt direkt die Abweichung für g vom Wert 2.
Wie aber misst man die Abweichung der Spinachse gegenüber der Bewegungsrichtung?
Dazu nutzt man aus, dass Myonen instabil sind und dass die beim Zerfall erzeugten Elektronen
bevorzugt in Myon-Spinrichtung ausgesandt werden.
Es dauert ungefähr 300 Umläufe, bis die Hälfte der kreisenden Myonen zerfallen ist, wobei man ausnutzt, dass hochenergetische Myonen sehr viel länger leben als ruhende Myonen (Grund ist die relativistische Zeitdilatation). Man misst also im Ring die Anzahl der in bestimmte Richtungen ausgesandten Elektronen über die Zeit. Die Zahl der gemessenen Elektronen nimmt dabei über die Zeit exponentiell ab, da immer weniger Myonen übrig bleiben und weiter kreisen. Dabei schwankt die Anzahl wellenförmig, je nachdem, ob die Myonenspins gerade in die richtige Richtung zeigen oder nicht. Es ergibt sich also für die Elektronenrate eine exponentiell abfallende Kurve, der eine schnelle wellenformige Oszillation überlagert ist. Aus der Frequenz dieser Oszillation (etwa eine Schwankung alle 30 Umläufe) ergibt sich dann die Abweichung des g-Faktors vom Wert 2.
Man hat dieses Experiment auch mit Antimyonen durchgeführt und denselben g-Faktor erhalten, wie es aufgrund des CPT-Theorems auch sein muss (siehe Kapitel 6.1 ).
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 31 December 2023