Wiederholen wir noch einmal jenen Satz aus Hilberts berühmtem Vortrag, in dem er seine Vision von den Grundlagen der Mathematik formuliert:
"Wenn es sich darum handelt, die Grundlagen einer Wissenschaft zu untersuchen, so hat man ein System von Axiomen aufzustellen, welche eine genaue und vollständige Beschreibung derjenigen Beziehungen enthalten, die zwischen den elementaren Begriffen jener Wissenschaft stattfinden. Die aufgestellten Axiome sind zugleich die Definitionen jener elementaren Begriffe und jede Aussage innerhalb des Bereiches der Wissenschaft, deren Grundlagen wir prüfen, gilt uns nur dann als richtig, falls sie sich mittels einer endlichen Anzahl logischer Schlüsse aus den aufgestellten Axiomen ableiten lässt."
Wie also müssen wir vorgehen, wenn wir diesen Satz als unseren Leitfaden wählen? Nehmen wir uns ein konkretes und Beispiel: die natürlichen Zahlen, also die Zahlen 1, 2, 3, 4, ... usw.. Normalerweise geht man davon aus, dass die natürlichen Zahlen unproblematisch und jedermann vom Abzählen und vom Anordnen her wohlbekannt sind. Doch wenn man genauer hinsieht, ist die Sache nicht mehr ganz so klar.
Stellen wir uns also die Frage "Was ist eigentlich eine natürliche Zahl?" Eine Antwort hierauf gab der italienische Mathematiker Giuseppe Peano (1858 - 1932) im Jahre 1889. Peano nannte fünf Eigenschaften, die die natürlichen Zahlen kennzeichnen (wir nehmen \( 0 \) (Null) zu den natürlichen Zahlen hinzu):
Man nennt diese Eigenschaften heute die Peano-Axiome.
Das erste Axiom besagt erst einmal allgemein, dass es eine natürliche Zahl Null gibt.
Das zweite Axiom drückt aus,
dass man beim Zählen immer einen Schritt weitergeht: von der 0 zur 1, von der 1 zur 2,
von der 2 zur 3 usw., wobei 1 der Nachfolger von 0 ist, 2 der Nachfolger von 1 usw..
Die Ziffern brauchen wir im Axiom aber nicht – es genügt der allgemeine Begriff des Nachfolgers.
Im dritten Axiom steht, dass man beim Zählen mit der Null anfängt
(man könnte natürlich auch mit Eins anfangen.
Diese ersten drei Axiome stellen gleichsam das Bildungsgesetz für natürliche Zahlen dar. Sie präzisieren den intuitiven Vorgang des Zählens mit einem Anfang (der Null) und dann Schritt für Schritt immer weiter.
Das vierte Axiom macht eine Aussage darüber, was Gleichheit von natürlichen Zahlen bedeutet.
Das letzte, sehr komplex wirkende Axiom schließlich wird Axiom der vollständigen Induktion genannt. Dieses Axiom überträgt das Bildungsgesetz der natürlichen Zahlen auf Eigenschaften der Zahlen. Es wird benötigt, wenn man eine Ausagen für alle natürlichen Zahlen beweisen will.
Überlegen wir genauer, was wir hier vor uns haben. Zunächst einmal beinhalten die Axiome gewisse Begriffe: natürliche Zahl, Null, Nachfolger, gleich, Eigenschaft, ... . Die Axiome stellen nun eine Reihe von Aussagen über diese Begriffe auf. Dabei wird an keiner Stelle einer der Begriffe irgendwie definiert. Die Definition erfolgt indirekt durch die aufgestellten Axiome.
Das obige Beispiel ist allerdings etwas irreführend, denn die Axiome sind in deutscher Sprache aufgeschrieben. Das bedeutet, dass wir intuitiv eine ganze Reihe von zusätzlichen Regeln anwenden, ohne sie explizit in Form von Axiomen aufgeschrieben zu haben. Diese Regeln spiegeln die Grammatik und den Wortschatz der deutschen Sprache wieder. Außerdem interpretieren wir unwillkürlich Begriffe wie Zahl und gleich, d.h. wir setzen sie in Beziehung zu dem Wissen, das wir über die entsprechenden Worte in unserer Sprache haben. Das ist jedoch in einem formalen Axiomensystem so nicht erlaubt, denn alles Wissen muss alleine in den Axiomen enthalten sein.
Man muss also versuchen, die Axiome ohne die Verwendung einer menschlichen Sprache zu formulieren. Dazu muss man eine künstliche (formale) Sprache definieren, indem man festlegt, welche Ausdrücke und Syntaxregeln in ihr gelten. Genau das macht man, wenn man eine Programmiersprache für Computer definiert, beispielsweise LISP, FORTRAN oder C.
Es würde hier zu weit führen, im Detail den ganzen formalen Apparat aufzubauen, den man für eine präzise Beschreibung der natürlichen Zahlen benötigt. Dieser Apparat ist recht umfangreich, denn jede Kleinigkeit muss in ihm erfasst werden – schließlich ist ein Rückgriff auf die deutsche Sprache oder auf Interpretationen von Begriffen nicht erlaubt! Eine detaillierte Beschreibung eines solchen formalen Systems findet man in Hofstadters Buch Gödel, Escher, Bach.
Überlegen wir daher nur prinzipiell, wie dieses System aussehen muss. Dabei lassen wir uns von der Analogie zu Computersprachen leiten.
Ein formales System (also eine formale Sprache) besteht zunächst aus einer Reihe von vorgegebenen Elementen (in Computersprachen wären das z.B. Schlüsselwörter wie IF, THEN, ELSE, BEGIN, END) – das ist der Wortschatz der Sprache. Einige Beispiele:
Es gibt Syntaxregeln, die es erlauben, die Elemente zu längeren Ausdrücken zusammenzusetzen – das ist die Grammatik der Sprache. Ausdrücke, die sich gemäß den Syntaxregeln aus den Elementen zusammensetzen, nennen wir wohlgeformt. In Computern überprüft beispielsweise ein Compiler, ob ein Computerprogramm wohlgeformt ist, d.h. ob es den Syntaxregeln entspricht. Dabei müssen die Syntaxregeln so beschaffen sein, dass man bei jedem Ausdruck in endlich vielen Schritten entscheiden kann, ob er wohlgeformt ist – analog muss ein Compiler immer entscheiden können, ob ein Computerprogramm den Syntaxregeln der Programmiersprache genügt. Das wird dadurch gewährleistet, dass die Syntaxregeln im Wesentlichen verlängernd wirken, d.h. eine Aussage lässt sich umgekehrt in ihre Bausteine zerlegen.
Weiter gibt es Umwandlungsregeln, die es erlauben, wohlgeformte Ausdrücke zu verändern, Ausdrücke zu kombinieren und so neue wohlgeformte Ausdrücke zu generieren. Die Umwandlungsregeln müssen also mit den Syntaxregeln verträglich sein. Dabei müssen diese Umwandlungsregeln nicht unbedingt verlängernd wirken. Sie können einen Ausdruck auch in zwei kleinere Ausdrücke zerlegen oder ihn irgendwie verkürzen bzw. die Zeichen in ihm umstellen. Daher ist nicht unmittelbar klar, wie und ob man durch Anwendung der Umwandlungsregeln von einem vorgegebenen wohlgeformten Ausdruck zu einem anderen vorgegebenen wohlgeformten Ausdruck kommt. Der Weg kann sehr verschlungen sein, wenn es ihn überhaupt gibt.
Ein Teil der Syntaxregeln und Umwandlungsregeln muss die Regeln der Logik (genauer: Aussagenlogik) widerspiegeln, denn in dem System sollen ja logische Schlussfolgerungen möglich sein.
Dazu legt man beispielsweise die folgenden vier Syntaxregeln fest: wenn die Ausdrücke \( A \) und \( B \) wohlgeformt sind, so betrachten wir auch die Ausdrücke
als wohlgeformt. Die obigen vier Regeln sind typische Syntaxregeln. Wie verlangt, wirken sie verlängernd, d.h. man kann umgekehrt die Wohlgeformtheit einer Aussage wie \( A \lor B \) auf die Wohlgeformtheit der kürzeren Aussagen \( A \) bzw. \( B \) zurückführen.
Neben den obigen Sytnaxregeln gibt es noch eine Reihe von Umwandlungsregeln, die die intuitiven Regeln der Logik wiederspiegeln. Hier einige Beispiele:
Bei diesen Regeln wird natürlich vorausgesetzt, dass \( A \) und \( B \) selbst wohlgeformt sind.
Über die Aussagenlogik und die damit mögliche Manipulation von Aussagen müsste noch einiges mehr gesagt werden. Dies wollen wir an dieser Stelle aber nicht weiter vertiefen – Details findet man beispielsweise in Hofstadters Buch.
Nun lassen sich in unserer formalen Sprache sehr viele wohlgeformte Ausdrücke zusammenstellen, auch solche, die – wenn man sie interpretiert – keine Wahrheit über natürliche Zahlen ausdrücken. Beispielsweise kann man 2+3=6 hinschreiben, genauso wie man in der deutschen Sprachen ebenfalls lügen kann.
An dieser Stelle kommen die Axiome ins Spiel. Sie bilden die wohlgeformten Start-Ausdrücke, die wir als wahr akzeptieren. Wir akzeptieren also ohne weitere Begründung, dass die fünf Peano-Axiome eine Wahrheit über die natürlichen Zahlen ausdrücken. Warum aber tun wir das?
Um den Begriff der Wahrheit ins Spiel zu bringen, ist es notwendig, aus dem formalen System hinauszuschauen und den Elementen der formalen Sprache eine Interpretation zu geben. Erst wenn wir den formalen Begriff natürliche Zahl mit unserem Verständnis von dem, was anschaulich eine natürliche Zahl sein soll, identifizieren, macht es überhaupt Sinn, einen Ausdruck unserer formalen Sprache als wahr oder falsch zu kennzeichnen. Dies ist ein ganz entscheidender Punkt! Erst die Interpretation der Begriffe eines formalen Systems ermöglicht es, von wahren und falschen Aussagen zu sprechen.
Wir akzeptieren also die Peano-Axiome als wahr, weil sie zu unserer anschaulichen Vorstellung von natürlichen Zahlen passen. Über diese Axiome versuchen wir ja gerade, ein formales System aufzubauen, dass die Eigenschaften der natürlichen Zahlen widerspiegelt. Weil die Peano-Axiome so wichtig sind für ein formales System der natürlichen Zahlen, wollen wir sie noch einmal in der oben definierten formalen Sprache dieses Systems notieren:
Das letzte Axiom ist das Axiom der vollständigen Induktion. Dabei ist \( A(n) \) irgendeine wohlgeformte Aussage des formalen Systems, in der die Variable \( n \) vorkommt. Es handelt sich bei dem letzten Axiom streng genommen um ein Axiomenschema, also um eine Art Axiomvorlage. Wie wir im nächsten Kapitel zeigen, sind die wohlgeformten Aussagen \( A(n) \) abzählbar, d.h. es gibt eine unendlich lange Liste aller Aussagen \( A(n) \). Analog dient das letzte Axiomenschema dazu, eine analoge Liste aller Axiome dieser Form zu erzeugen, indem man die einzelnen \( A(n) \) der Reihe nach einsetzt. Man spricht auch von den Instanzen des Schemas.
Beachten Sie, dass wir im letzten Axiom nicht so etwas wie \( \forall A(n) \) geschrieben haben! Im obigen formalen System können wir nämlich nicht über alle Aussagen der natürliche Zahlen sprechen, sondern nur über alle natürlichen Zahlen, also beispielsweise \( \forall n \). Will man etwas über alle Aussagen der natürliche Zahlen aussagen, dann braucht man ein mächtigeres formales System, beispielsweise die Mengenlehre.
Die Peano-Axiome alleine reichen noch nicht aus, um das Addieren und Multiplizieren von natürlichen Zahlen zu ermöglichen. Daher benötigt man weitere Axiome, die dazu genauere Aussagen machen:
Auf diese wohlgeformten Startausdrücke (Axiome) können wir nun die Umwandlungsregeln unserer formalen Sprache anwenden und so neue wohlgeformte Ausdrücke erzeugen. Wenn nun unsere Axiome die natürlichen Zahlen gut charakterisieren, und wenn die Regeln logischen Schlussfolgerns Teil der Regeln unseres formalen Systems sind, so erwarten wir, dass alle so erzeugten Ausdrücke Wahrheiten über die natürlichen Zahlen ausdrücken, wenn wir die darin enthaltenen Begriffe entsprechend interpretieren. Es zeigt sich, dass dies tatsächlich der Fall ist. In diesem Sinne können wir also neue Wahrheiten über natürliche Zahlen beweisen, indem wir die entsprechenden formalen Ausdrücke durch das mechanische Anwenden von Umwandlungsregeln aus den Start-Ausdrücken erzeugen.
Hilbert aber ging in seinem Vortrag noch weiter:
Oben hatten wir gesagt, dass wir jede Aussage, die sich mit dem formalen System ausgehend von den Axiomen erzeugen lässt, nach der Interpretation als Wahrheit über die natürlichen Zahlen akzeptieren können. Die interpretierten Aussagen entsprechen dem, was wir von natürlichen Zahlen erwarten."... jede Aussage innerhalb des Bereiches der Wissenschaft, deren Grundlagen wir prüfen, gilt uns nur dann als richtig, falls sie sich mittels einer endlichen Anzahl logischer Schlüsse aus den aufgestellten Axiomen ableiten lässt."
Hilbert fordert das Umgekehrte: Alles, was wir als Wahrheit über die natürlichen Zahlen akzeptieren, muss sich als Aussage in unserem formalen System aus den Axiomen erzeugen lassen! Es genügt nicht, dass die entsprechende formale Aussage wohlgeformt ist (d.h. den Grammatikregeln entspricht), denn auch falsche Aussagen können wohlgeformt sein, also der formalen Grammatik entsprechen.
Wie wir aus dem Vorwort bereits wissen, geht Hilberts Wunsch nicht in Erfüllung. Es gibt wohlgeformte Aussagen (nennen wir sie \( A \) ), die sich nicht aus den Axiomen erzeugen lassen. Auch deren Gegenteil (also die Aussage \( \neg A \) ) lässt sich nicht erzeugen. Das formale System sagt uns also nicht, ob wir diese Aussage als wahr oder falsch zu bewerten haben.
Was aber ist die Aussage nun: wahr oder falsch? Die Antwort auf diese Frage hängt von der Interpretation ab, die wir den Symbolen des formalen Systems geben.
Ein Beispiel für verschiedene Interpretationsmöglichkeiten bietet das folgende Axiomensystem, das (in etwas anderer Form) vor mehr als 2000 Jahren von dem Griechen Euklid formuliert wurde:
Diese Axiome sind wieder in deutscher Sprache angegeben, d.h. sie genügen nicht den strengen Kriterien, die wir oben an ein formales System mit formaler Sprache gestellt haben. Ich habe aber absichtlich gewisse Begriffe nicht wie üblich ausgeschrieben, sondern durch die formalen Begriffe (Buchstaben) \(P, G, A, K\) und \(R\) abgekürzt, um zu verhindern, dass wir sie unmittelbar interpretieren.
Was könnte nun eine sinnvolle Interpretation für diese Begriffe sein, so dass die fünf Axiome einen Sinn ergeben und wir sie als wahr akzeptieren?
Wie wäre es mit folgendem Vorschlag:
Ob diese Interpretation passt, sehen wir am Besten, wenn wir die formalen Begriffe in den Axiomen durch die Interpretationen ersetzen:
Diese Aussagen entsprechen unserer Anschauung von Punkten, Geraden, Kreisen, Abständen und Winkeln in einer zweidimensionalen Ebene. Euklid hatte um 300 vor Christus diese fünf Axiome (in etwas anderer Formulierung) in seinen dreizehn Büchern der Elemente aufgestellt und aus ihnen praktisch das gesamte damals bekannte Wissen über Geometrie abgeleitet. Man bezeichnet dieses Teilgebiet der Mathematik deshalb als Euklidische Geometrie. Die Elemente Euklids sind bis heute das erfolgreichste Werk der mathematischen Weltliteratur, und es ist selbst nach 2300 Jahren immer noch erhältlich.
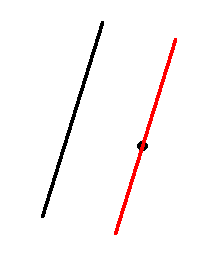
Das fünfte Axiom bezeichnet man auch als Parallelenaxiom.
Es besagt, dass man zu einer vorgegebenen Geraden genau eine dazu parallele Gerade
durch einen vorgegebenen Punkt zeichnen kann.

Dieses Axiom bereitete den Menschen über viele Jahrhunderte hinweg Kopfzerbrechen. Man vermutete, dass die ersten vier Axiome bereits alles enthalten sollten, was es über Punkte, Geraden, Kreise, Abstände und Winkel zu sagen gibt. Daher versuchte man, das fünfte Axiom aus den ersten vier Axiomen abzuleiten – ohne Erfolg.
Erst in den Jahren zwischen 1800 und 1850 entdeckte man, dass es ohne das fünfte Axiom auch andere Möglichkeiten gibt, die formalen Begriffe in den ersten vier Axiomen zu interpretieren. Das fünfte Axiom ist unabhängig von den anderen vier Axiomen. Was also passiert, wenn wir das fünfte Axiom durch ein anderes Axiom ersetzen, beispielsweise durch folgendes Axiom:
Unsere obige Interpretation würde nun eine Aussage über Geraden machen, die wir nicht akzeptieren:
Wir würden widersprechen, denn wir können eben genau eine solche Gerade zeichnen; sie liegt parallel zur vorgegebenen Geraden. Ist also das Postulat dann falsch?
Wie wäre es mit folgender Interpretation:
Die anderen Interpretationen bleiben weitgehend unverändert. Schauen wir uns die entsprechenden Interpretationen der Postulate an:
Das so festgelegte Teilgebiet der Mathematik nennt man Elliptische Geometrie.
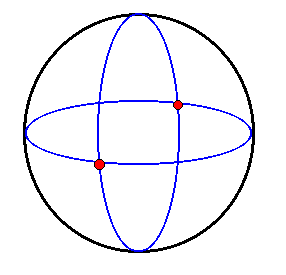
Über das dritte Postulat müsste man dabei kurz nachdenken: man kann sich das Punktepaar wie Nord- und Südpol
vorstellen und den Kreis wie einen Breitengrad, wobei man als Abstand den minimalen Abstand zu einem
der Pole verstehen könnte. Wichtiger aber ist, dass nun auch das veränderte fünfte Postulat eine
wahre Aussage über Punktepaare und Großkreise auf der Kugel macht: zwei Großkreise schneiden sich immer,
d.h. es gibt keine parallelen Großkreise.
Es gibt sogar noch eine dritte Möglichkeit für das fünfte Axiom:
Man spricht von der Hyperbolischen Geometrie. Man kann sich diese Form der Geometrie beispielsweise durch Linien und Punkte auf einer Satteloberfläche veranschaulichen.
Wir sehen also, dass die Axiome selbst zunächst weder wahr noch falsch sind. Erst über eine Interpretation werden sie wahr oder falsch. Innerhalb eines formalen Systems (also ohne Interpretation der Begriffe) können wir also von Wahrheit noch gar nicht sprechen. Wir können lediglich fordern, dass die Axiome widerspruchsfrei sind, d.h. dass sich innerhalb des formalen Systems nicht eine Aussage \( A \) und die gegenteilige Aussage \( \neg A \) erzeugen lässt. Ohne diese Minimal-Forderung kommt man allerdings nicht aus, wenn man die Regeln der gewohnten Logik in das formale System integriert – ansonsten werden schnell beliebige Aussagen erzeugbar und eine brauchbare Interpretation erscheint nicht mehr möglich.
Das obige Beispiel macht noch etwas anderes deutlich:
Die im formalen System verwendeten Begriffe werden an keiner Stelle definiert. Sie sind zunächst bedeutungsleere Zeichenketten. Eine Definition müsste die formalen Begriffe ja durch andere Begriffe erklären, deren Bedeutung feststeht. Solche Begriffe gibt es aber erst einmal in einem uninterpretierten formalen System nicht, d.h. eine Definition könnte bestenfalls eine Art Abkürzung festlegen, genauso wie man in Computerprogrammen Includes verwendet. Die Bedeutung der Begriffe entsteht durch die Gesamtheit der Axiome und die Art, wie in ihnen mit den formalen Begriffen umgegangen wird. Dabei ist es durchaus möglich, dass verschiedene Interpretationen (Bedeutungen) möglich sind. So kann man in einem System, dass nur die ersten vier Axiome Euklids umfasst, \( G \) als Gerade in der Ebene oder als Großkreis auf der Kugel deuten. Je nachdem, welches fünfte Axiom man hinzufügt, wird die Bedeutung in die eine oder andere Richtung festgelegt.
Dies ist in der Umgangssprache nicht viel anders. Ein Kind, das seine Muttersprache erlernt, bekommt von seinen Eltern auch keine Definitionen serviert. Es lernt die Bedeutung der Worte aus der Art, wie sie in Sätzen und in verschiedenen Situationen verwendet werden. Normalerweise merkt sich ein kleines Kind auch nicht nur einen isolierten Begriff, sondern gleich einen ganzen Satz und eine Situation dazu. Ein authentisches Beispiel von einem Waldspaziergang: "Mama, sieh mal eine Regenrinne – da läuft das Wasser durch." Und auch in der Umgangssprache gibt es manchmal die Möglichkeit, dass ein Wort mehrere Bedeutungen haben kann. Man denke an das Wort Schloss, dessen Bedeutung erst durch den Zusammenhang, in dem es verwendet wird, festgelegt wird (der König wohnt im Schloss, aber sein Schlüssel passt nicht ins Schloss). Ein anderes schönes Beispiel ist das Wort Gift: ein Deutscher denkt dabei an Vergiften, ein Engländer an ein Geschenk.
Ich hoffe, es ist mir gelungen, Ihnen in diesem Kapitel den Begriff des formalen Systems näherzubringen und die vielen Fallgruben anzudeuten, in die man geraten kann, wenn man Interpretationen der Begriffe zu früh ins Spiel bringt. Wir sind nun gerüstet, um uns im Weiteren Hilberts Vision zuzuwenden und zu verstehen, warum sie scheitern muss.
© Jörg Resag, www.joerg-resag.de
last modified on 20 February 2023