Im vorhergehenden Kapitel 5.9
sind wir bei der RSA-Verschlüsselung auf ein interessantes
mathematisches Objekt gestoßen:
die multiplikative Gruppe modulo N
(
prime Restklassengruppe), abgekürzt als
\(\mathbb{Z}_N^*\) .
Diese Gruppe besteht aus allen natürlichen Zahlen von \(1\) bis \(N\), die teilerfremd
zu \(N\) sind (wobei \(1\) als teilerfremd zu \(N\) zählt).
Für \( N = 15 = 3 \cdot 5 \) sähe diese Gruppe also so aus:
\[
\mathbb{Z}_{15}^* = \{ 1, 2, 4, 7, 8, 11, 13, 14 \}
\]
Alle Vielfachen der Teiler \(3\) und \(5\) lassen wir also weg, so dass von den 15 Zahlen
nur die obigen 8 Zahlen übrig bleiben.
Eine Gruppe wird diese Zahlenmenge dadurch, dass wir
die folgende Gruppenoperation (nennen wir sie \( \circ \) )
einführen:
\[
a \circ b := (a \cdot b) \;\mathrm{mod}\; N
\]
Die beiden Zahlen \(a\) und \(b\) aus der Gruppe werden also miteinander multipliziert,
und anschließend wird noch ein möglichst großes Vielfaches von \(N\) abgezogen
(das bedeutet modulo \(N\), kurz \(\mathrm{mod}\; N\)).
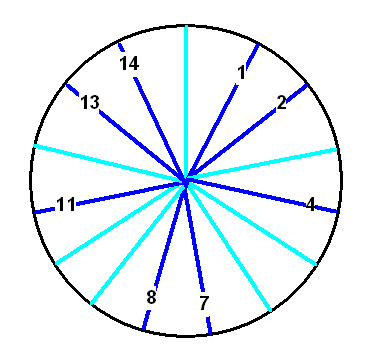
Wir hatten diese Gruppe als Rad mit \(N\) durchnummerierten Speichen dargestellt,
wobei wir alle Speichen weglassen, deren Speichennummer nicht teilerfremd
zu \(N = 15\) ist. Hier ist das entsprechende Rad für \(N = 15\), wobei
die hellblauen Speichen nicht zur Gruppe gehören:

Eine Multiplikation mit \(4\) modulo \(15\) bedeutet in diesem Bild: Aus der Speiche 1 wird die Speiche 4, aus der Speiche 2 wird die Speiche 8, aus der 4 wird die 1 (denn die 16 liegt nach einem Umlauf wieder auf der 1), aus der 7 wird die 13 (denn die 28 liegt nach einem Umlauf auf der 13) etc.. Man kann sich vorstellen, dass man die Speichennummern auf ein Gummiband schreibt, das zu Beginn einmal um das Rad gewickelt ist. Multiplikation mit \(4\) modulo \(15\) bedeutet, dass man das Gummiband auf das Vierfache dehnt und dann 4 mal um das Rad wickelt.
Die RSA-Verschlüsselung verwendet ein Rad mit extrem vielen Speichen und wiederholt das Dehnen und Aufwickeln mehrere tausend mal, was zu einer sehr guten Vermischung aller Speichen führt, die man ohne einen Trick nicht so einfach wieder entwirren kann. Mehr dazu im vorhergehenden Kapitel 5.9.
An diesem Beispiel sehen wir bereits alles, was eine Gruppe ausmacht:
Die Eigenschaften einer Gruppe:
|
Die Gruppe \(\mathbb{Z}_N^*\) erfüllt alle diese Eigenschaften, wie wir in Kapitel 5.9 gesehen haben (was insbesondere beim inversen Element gar nicht so einfach war). So ist im obigen Beispiel mit \(N = 15\) das inverse Element zur \(7\) die \(13\), denn \( 7 \cdot 13 = 91 \), was modulo \(15\) (also nach Abzug von \(6 \cdot 15 = 90\)) wie gewünscht \(1\) ergibt.
Gruppen treten in der Mathematik und Physik an sehr vielen Stellen in Erscheinung. Kaum ein anderer Begriff ist so wichtig und universell wie der Begriff der Gruppe. So bilden beispielsweise die Rotationen im dreidimensionalen Raum eine Gruppe, denn zwei Rotationen ergeben zusammen wieder eine Rotation, man kann Rotationen beliebig zusammenfassen (klammern), es gibt zu jeder Rotation eine Gegen-Rotation und man kann auch gar nichts tun (Rotation um Null Grad, also das neutrale Element). Mehr dazu siehe in die Symmetrie der Naturgesetze.
Nun sind Rotationen und viele andere in der Physik wichtige Gruppen sogenannte kontinuierliche Gruppen. So gibt es kontinuierlich viele Drehwinkel, um die man drehen kann. Viele diese Gruppen haben wir in die Symmetrie der Naturgesetze bereits ausführlich dargestellt.
Die obige Gruppe \(\mathbb{Z}_N^*\) ist dagegen
ein Beispiel für eine diskrete und sogar endliche Gruppe, d.h. sie
besteht aus endlich vielen einzelnen Gruppenelementen.
Solche endlichen Gruppen können beispielsweise als Symmetriegruppen von
Kristallen auftreten (d.h. hier machen nur bestimmte Drehwinkel Sinn).
Ein anderes wohlbekanntes Beispiel ist
Rubik's Cube (Zauberwürfel). Die Verdrehungen der verschiedenen Ebenen dieses Würfels
bilden zusammen ebenfalls eine endliche Gruppe.

Quelle: Wikimedia Commons File:F2LUp.svg,
dort Public Domain.
Nun könnte man meinen, endliche Gruppen seien nicht allzu komplex – schließlich enthält jede von ihnen nur endlich viele Elemente. Unsere obige Beispielgruppe \( Z_{15}^* \) enthält sogar nur 8 Elemente und ist tatsächlich recht übersichtlich. Doch das täuscht! Rubiks Zauberwürfel-Gruppe enthält beispielsweise ungefähr \( 4,3 \cdot 10^{19} \) Elemente, d.h. so viele verschiedene Würfel-Konfigurationen lassen sich aus der Grundstellung durch mehrfache Drehungen der einzelnen Würfelebenen erzeugen. Zum Vergleich: So viele Gasmoleküle sind in etwa 1,6 ml Luft in unserer Umgebung enthalten. Das ist eine recht große Zahl, und entsprechend schwierig ist es, einen verdrehten Zauberwürfel durch bloßes Herumprobieren wieder in seine Ausgangskonfiguration zurückzudrehen – man verirrt sich unweigerlich in der großen Zahl der Möglichkeiten. Es ist gar nicht so leicht, eine Folge von Drehungen zu finden, mit der sich eine bestimmte Würfelkonfiguration aus der Grundstellung heraus erzeugen lässt (oder umgekehrt diese Würfelkonfiguration wieder in die Grundstellung überführen lässt), besonders wenn man eine möglichst kurze Zugfolge haben möchte. Daran erkennt man, dass die entsprechende Zauberwürfel-Gruppe bereits eine recht komplexe Struktur hat, auch wenn sie endlich ist.
Ist es möglich, eine komplette Übersicht über alle denkbaren endlichen Gruppen anzugeben? Anders ausgedrückt: Kann man diese Gruppen komplett klassifizieren, so dass man in einer langen Liste jeden möglichen Gruppentyp wiederfindet? Es hat sich gezeigt, dass dieses Ziel mit heutigen Mitteln in unerreichbarer Ferne liegt. Es gibt einfach zu viele Möglichkeiten, Gruppen aus endlich vielen Objekten zu bilden. Endliche Gruppen können eben sehr viele Elemente enthalten, die auf extrem komplexe Weise miteinander verbunden sein können.
Trotz dieser Komplexität ist die Sache allerdings nicht ganz hoffnungslos, wenn man das Ziel etwas bescheidener wählt. Es ist nämlich gelungen, einen kompletten Satz von Bausteinen zu finden, aus denen sich alle endlichen Gruppen im Prinzip zusammensetzen lassen. Allerdings kann dieses Zusammensetzen kompliziert sein, so dass man aus den Bausteinen nicht alle Eigenschaften der daraus gebildeten Gruppen ableiten kann. Diese Bausteine sind die sogenannten einfachen Gruppen, wobei diese einfachen Gruppen teilweise höchst komplex sein können (das Wort einfach ist also etwas irreführend).
Seit dem Jahr 1982 besitzt man eine vollständige Übersicht über die einfachen Gruppen – man sagt, die einfachen Gruppen sind vollständig klassifiziert. Da auch einfache Gruppen sehr komplex sein können, war es keineswegs einfach, diese komplette Übersicht zu erstellen: Viele Mathematiker waren über 30 Jahre lang damit beschäftigt, die einzelnen Mosaiksteinchen in über 500 Fachartikeln auf über 15000 Druckseiten zusammenzutragen. Bis 2002 arbeitete man daran, den Beweis zusammenhängend auf rund 1200 Seiten darzustellen (Aschbacher, Smith: The classification of quasithin groups, AMS). Obwohl vermutlich kaum jemand heute einen kompletten Überblick über diesen sehr langen Beweis hat, ist man sich doch mittlerweile relativ sicher, dass keine Lücken mehr darin vorhanden sind (eine absolute Garantie gibt es allerdings nicht – auch Mathematiker sind nur fehlbare Menschen).
Es kann hier nicht das Ziel sein, auf diesen Beweis näher einzugehen (ich bin auch kein Experte auf diesem Gebiet). Was wir aber versuchen wollen, ist zu verstehen, was einfache Gruppen eigentlich sind, welche einfachen Gruppen es in der kompletten Übersicht gibt und wie aus ihnen endliche Gruppen zusammengesetzt werden können. Mal sehen, auf was für exotische Objekte wir dabei stoßen werden.
Endliche Gruppen kann man in einfache Gruppen zerlegen (Details weiter unten). Entsprechend sind einfache Gruppen dadurch gekennzeichnet, dass man sie nicht in noch einfachere Gruppen zerlegen kann. Ein Analogon wären die Atome chemischer Elemente: jedes Molekül ist aus Atomen chemischer Elemente aufgebaut (so wie jede endliche Gruppe aus einfachen Gruppen zusammengesetzt ist), und ein Atom lässt sich nicht in noch einfachere Atome zerlegen. Auch bei Molekülen reicht es übrigens nicht aus, nur die Atome zu kennen, aus denen sie bestehen. Es kommt auch darauf an, wie diese Atome zusammengefügt sind – man denke an die großen Moleküle komplexer organischer Verbindungen. Bei endlichen Gruppen ist es ähnlich.
Es gibt mehrere gleichwertige Möglichkeiten, einfache Gruppen genauer zu definieren. Wir hatten gerade gesagt, dass eine einfache Gruppe keine kleineren Gruppen mehr enthalten darf. Das kann man präzisieren, indem man kleinere Gruppe durch normale Untergruppe (auch Normalteiler genannt) ersetzt. Was also ist eine normale Untergruppe?
Nun, zunächst ist eine Untergruppe einer gegebenen Gruppe einfach eine Teilmenge der Gruppe, wobei die Gruppenelemente dieser Teilmenge wieder alle obigen Gruppeneigenschaften aufweisen. Das neutrale Element muss also in dieser Teilmenge liegen, es muss jeweils ein inverses Element geben und das Gruppenprodukt \( a \circ b \) darf nicht aus dieser Teilmenge hinausführen (statt \( a \circ b \) werden wir auch vereinfacht \( a b \) schreiben). Bei Rubiks Zauberwürfel kann man beispielsweise leicht Untergruppen erzeugen, indem man nur noch die Drehung bestimmter Würfelebenen zulässt, während man die anderen Würfelebenen fixiert.
Damit eine Untergruppe (nennen wir sie \(N\)) einer gegebenen Gruppe (nennen wir sie \(G\)) normal ist, muss sie zusätzlich noch die folgende Bedingung erfüllen (diese Bedingung brauchen wir weiter unten, um \(G\) mit Hilfe von \(N\) in einzelne Scheiben zu zerlegen und zwischen diesen Scheiben eine Gruppenstruktur definieren zu können):
|
normale Untergruppen (Normalteiler): Wir nehmen ein beliebige Element \(g\) aus einer gegebenen Gruppe \(G\) und ein beliebiges Element \(n\) aus einer Untergruppe \(N\) von \(G\). Wenn dann das Gruppenelement \[ g n g^{-1} \] stets immer noch in der Untergruppe \(N\) liegt, dann ist \(N\) eine normale Untergruppe (Normalteiler) von G. Es gibt also ein Element \(n'\) in \(N\), so dass \( g n g^{-1} = n' \) ist oder umgestellt: \[ g n = n' g \] |
Diese Zusatzbedingung ist nur dann wichtig, wenn das Kommutativgesetz für die Gruppe \(G\) nicht gilt, d.h. wenn man die Reihenfolge zweier Gruppenelemente in \( g g' \) nicht allgemein umdrehen darf. Das ist beispielsweise bei Rubiks Zauberwürfel-Gruppe der Fall: dreht man zwei verschiedene Ebenen, die eine gemeinsame Kante haben, so kommt es auf die Reihenfolge der beiden Drehungen an! Bei unserer Gruppe \(\mathbb{Z}_N^*\) von oben gilt dagegen das Kommutativgesetz – man spricht von einer abelschen Gruppe. In einer abelschen Gruppe ist \[ g n g^{-1} = n g g^{-1} = n 1 = n \] was natürlich automatisch in der Untergruppe \(N\) liegt. In einer abelschen Gruppe \(G\) ist also jede Untergruppe \(N\) zugleich auch eine normale Untergruppe (Normalteiler).
Schauen wir uns ein nicht-abelsches Beispiel an: Beim Zauberwürfel gibt es eine Untergruppe von Zugfolgen, die die einzelnen Steine (also die 8 Ecksteine, die 12 Kantensteine und die 6 Mittelsteine) jeweils an ihrem Platz belässt, aber deren Orientierung ändert, also Ecken und Kanten kippt (bei Mittelsteinen kann man nichts kippen). So kann man durch Zugfolgen aus dieser Untergruppe beispielsweise 2 Ecken oder 2 Kantensteine kippen (Anmerkung: einen einzelnen Eckstein oder Kantenstein kann man nicht kippen).
Diese Kipp-Untergruppe ist ein Normalteiler, wie man so sieht: Nehmen wir irgendeine Zugfolge \(g\) aus der Gesamt-Gruppe, die Steine vertauscht (und ggf. auch kippt), sowie eine Zugfolge \(n\) aus unserer Untergruppe, die nur Steine kippt. Bei \( g n g^{-1} \) (von rechts nach links gelesen und ausgeführt) vertauscht dann \( g^{-1} \) die Steine, \(n\) kippt sie und \(g\) tauscht sie wieder zurück, so dass insgesamt \( g n g^{-1} \) auch nur Steine kippt (es spielt keine Rolle, wenn \(g\) auch noch Steine kippt). Also ist \( g n g^{-1} \) wieder ein Element unserer Kipp-Untergruppe. Außerdem ist die Untergruppe sogar abelsch, denn beim Kippen spielt die Reihenfolge keine Rolle. Mehr dazu siehe Wikipedia: Rubik's Cube group.
Auch die Zauberwürfel-Untergruppe, die nur die Ecksteine beeinflusst (kippt und/oder vertauscht), ist ein Normalteiler: Bei \( g n g^{-1} \) manipuliert \( g^{-1} \) Ecken und Kanten, \(n\) manipuliert nur die Ecken und \(g\) macht die Kanten-Manipulation von \( g^{-1} \) wieder rückgängig, so dass insgesamt \( g n g^{-1} \) nur Ecken manipuliert (siehe Wikipedia: Normal subgroup).
Andere Untergruppen wie beispielsweise die Drehungen nur einer einzelnen Ebene sind dagegen keine Normalteiler.
Was ist nun eine einfache Gruppe? Sie darf keine kleineren normalen Untergruppen enthalten, oder anders gesagt: Die einzigen erlaubten normalen Untergruppen sind diejenigen, die immer da sind, nämlich die Gruppe selbst sowie die triviale Gruppe (die nur aus dem neutralen \(1\)-Element besteht). Außerdem darf eine einfache Gruppe nicht gleich der trivialen Gruppe \( \{1\} \) sein. Mehr dazu siehe auch in Wikipedia: Simple group. Halten wir also fest:
|
einfache Gruppen: Einfache Gruppen sind nicht-triviale Gruppen, die außer sich selbst und der trivialen Gruppe keine anderen normalen Untergruppen besitzen.
|
Betrachten wir eine nicht-einfache endliche Gruppe \(G\), die also eine kleinere normale Untergruppe \(N\) enthält. Dann können wir diese Gruppe in zwei kleinere Gruppen zerlegen, nämlich in die normale Untergruppe \(N\) und die sogenannte Faktorgruppe (Quotientengruppe oder englisch quotient group, mit \(G/N\) bezeichnet und meist als \(G\) modulo \(N\) gesprochen) – wie das geht, kommt gleich.
Diesen Zerlegungs-Prozess kann man mehrfach wiederholen und so zu immer kleineren Gruppen vordringen. Bei endlichen Gruppen erhält man so schließlich eine endliche Liste von eindeutig bestimmten einfachen Gruppen, aus denen sich unsere Ursprungsgruppe zusammensetzt ( Jordan-Hölder-Theorems). In diesem Sinn sind die einfachen Gruppen in dieser Liste die Bausteine unserer endliche Gruppe. Allerdings wird die Struktur der endlichen Gruppe nicht alleine durch die einfachen Gruppen in der Baustein-Liste festgelegt, denn auch die Art der Zusammensetzung der einfachen Gruppen zur Gesamtgruppe spielt eine Rolle.
Nun zu den Details der angesprochenen Zerlegung. Die Idee ist, die normale Untergruppe \(N\) aus \(G\) gleichsam herauszuziehen und dabei die Gruppe \(G\) gewissermaßen zur kleineren Gruppe \(G/N\) einzudampfen. Dabei kollabiert \(N\) selbst zum \(1\)-Element in \(G/N\). Man kann es sich auch so vorstellen: Man zerlegt \(G\) in einzelne Scheiben (auch Nebenklassen genannt), wobei eine dieser Scheiben die normale Untergruppe \(N\) ist. Diese Scheiben sind nun die Elemente der kleineren Gruppe \(G/N\), wobei sich die Gruppenstruktur in \(G/N\) deshalb ergibt, weil \(N\) eine normale Untergruppe ist. Die \(N\)-Scheibe spielt dabei die Rolle des \(1\)-Elementes in \(G/N\). Siehe dazu auch Wikipedia: Quotient Group.
Machen wir es konkreter: Eine der Scheiben von \(G\) ist die normale Untergruppe \(N\). Alle anderen Scheiben erreichen wir, indem wir passende Gruppenelemente \(g \in G\) an die Elemente von \(N\) heranmultiplizieren, wobei wir uns für ein Heranmultiplizieren von links entscheiden. Es ist naheliegend, so eine Scheibe mit \( g N \) zu bezeichnen, d.h. alle Elemente \(h \in g N \) lassen sich in der Form \[ h = gn \] schreiben mit einem passenden \(n \in N\) und dem vorgegebenen \(g \in G\). Auch \(g\) selbst liegt – gleichsam als Ankerpunkt – in der Scheibe \( g N \), denn das neutrale Element \(1\) liegt ja in der Untergruppe \(N\) und wenn wir \(n = 1\) wählen, dann ist \[ g = g1 \] Wenn wir nun für \(g\) alle möglichen Elemente aus \(G\) zulassen, so überdecken wir die gesamte Gruppe \(G\) mit \( g N \)-Scheiben, wobei viele verschiedene \(g\) dieselbe Scheibe ergeben werden Die beiden Scheiben \(gN\) und \(hN\) sind nämlich dann identisch, wenn \(h = gn\) ist, denn dann liegt auch \(h\) in derselben Scheibe wie \(g\) und kann als alternativer Ankerpunkt verwendet werden. Sowohl \(g\) als auch \(h\) kann man als Repräsentanten für die Scheibe verwenden. Die \(N\)-Scheibe selbst kann man dabei durch die \(1\) repräsentieren, die in \(N\) liegt.
Betrachten wir zwei Gruppenelemente \(g\) und \(g'\), die nicht aus derselben Scheibe stammen, sodass \( g N \) und \( g' N \) unterschiedliche Scheiben darstellen. Die Elemente dieser beiden Scheiben können wir dann immer als \( g n \) und \( g' n' \) schreiben mit passenden \(n, n'\in N\). Was geschieht nun, wenn wir zwei solche Gruppenelemente aus verschiedenen Scheiben miteinander multiplizieren? Rechnen wir es nach: \[ (g n) \, (g' n') = g n g' n' = \, ... \] Jetzt verwenden wir, dass \(N\) eine normale Untergruppe ist, d.h. es gibt ein Element \(n'' \in N\) mit \( n g' = g' n'' \). An dieser Stelle sieht man, warum man normale Gruppen gerade so wie oben angegebenen definiert hat, denn nur mit dieser Definition kommen wir hier weiter und können nach einigen Schritten eine Gruppenstruktur auf \(G/N\) definieren. Rechnen wir also weiter: \[ ... \, = g g' n'' n = (g g') n''' \] mit einem Element \( n''' = n'' n \) aus \(N\), sodass unser Ergebnis in der Scheibe \( (g g') N \) liegt. Das Produkt eines Elementes aus der Scheibe \( g N \) mit einem Element aus der Scheibe \( g' N \) ergibt also immer ein Element aus der Scheibe \( (g g') N \).
Dabei spielt es keine Rolle, welchen Repräsentanten wir aus den beiden Scheiben wählen – das Produkt liegt immer in der Scheibe \( (g g') N \). Umgekehrt lässt sich auch jeder Repräsentant \( (g g') n''' \) aus der Scheibe \( (g g') N \) so erreichen, denn jedes \( n''' \) lässt sich als Produkt \( n''' = n'' n \) schreiben.
Eigentlich ist uns egal, welches \(n'''\) sich genau ergibt – wir wollen die Gruppe \(N\) gleichsam vergessen und uns nur dafür interessieren, in welcher Scheibe die Elemente liegen. Dann können wir auch schreiben: \[ (g N) \, (g'N) := (g g') N \] was formal das Produkt links zwischen den beiden Scheiben \( g N \) und \( g' N \) definiert. Es bedeutet, dass ein Element aus Scheibe \( g N \) mal einem Element aus Scheibe \( g' N \) immer ein Element aus Scheibe \( (g g') N \) ergibt, wobei uns nicht das genaue Element, sondern nur seine Scheiben-Zugehörigkeit interessiert.
Man kann nun leicht nachrechnen, dass dieses Produkt zwischen Scheiben alle Gruppeneigenschaften aufweist. Die Scheibe \(N\) spielt dabei die Rolle des \(1\)-Elementes, denn wir können sie auch als \( 1 N \) schreiben. Bezeichnen wir die Menge aller Scheiben mit \(G/N\), so bildet diese Menge zusammen mit dem obigen Scheiben-Produkt eine Gruppe, die auch als Faktorgruppe oder Quotientengruppe bezeichnet wird.
Ein Beispiel: Oben hatten wir gesehen, dass bei Rubiks Zauberwürfel die Manipulationen der Ecksteine eine normale Untergruppe bilden. Die Faktorgruppe \(G/N\) entspricht dann den Manipulationen, bei denen uns die Ecksteine egal sind – das wären dann die Manipulationen der Kantensteine bei beliebiger Veränderung der Ecksteine (die Mittelsteine können wir festhalten, da ihre Manipulation nur anderen Orientierungen des Würfels im Raum entspricht).
Wenn man nun die beiden Gruppen \(N\) und \(G/N\) kennt, kann man damit die ursprüngliche Gruppe \(G\)
rekonstruieren? Naheliegend wäre irgendein Produkt der Form \( G = N \cdot G/N \).
Es gibt tatsächlich solche Produkte, beispielsweise das direkte oder das semidirekte Produkt
(siehe auch weiter unten).
Aber nicht jede Gruppe \(G\) ist gleich einem solchen Produkt aus \(N\) und \(G/N\).
Man verliert also bei der Zerlegung der Gruppe \(G\) in die normale Untergruppe \(N\),
die die Elemente innerhalb jeder Scheibe verbindet, und in die
Faktorgruppe \(G/N\), die zwischen den Scheiben wirkt, Informationen
über \(G\). Kennt man nur \(N\) und \(G/N\), so weiß man
nur bei Gruppenelementen in der \(N\)-Scheibe,
was ihr Produkt genau ergibt. Liegen die Gruppenelemente
in verschiedenen Scheiben, so sagt einem die Gruppe \(G/N\) nur, in welcher Scheibe
ihr Produkt landet, aber nicht genau, an welcher Stelle.
Mehr dazu siehe in
Wikipedia: Extension Problem.
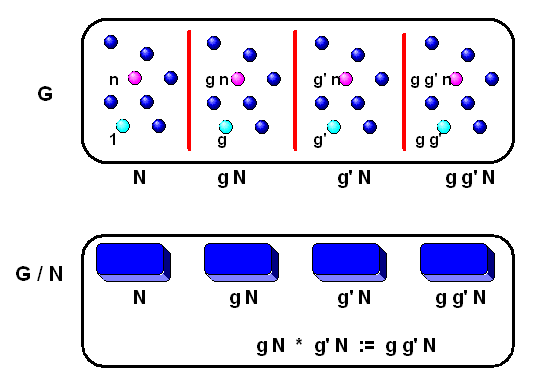
Das obige Bild zeigt noch eine wichtige Eigenschaft der Zerlegung: Jede Scheibe ist gleich groß und enthält genauso viele Elemente wie die Untergruppe \( N \), denn jedes Element \(h\) einer Scheibe \( g N \) lässt sich eindeutig als \( h = g n \) mit festem \(g\) schreiben und so eindeutig einem Element \(n \in N\) zuordnen. Außerdem überlappen die Scheiben nicht, d.h. jedes Element aus \(G\) liegt eindeutig in einer bestimmten Scheibe. Die Anzahl Scheiben mal die Anzahl Elemente pro Scheibe muss also gleich der Gesamtanzahl Elemente in \(G\) sein:
|
Satz von Lagrange: Wir bezeichnen mit \( |G| \) die Anzahl der Elemente (die sogenannte Ordnung) der endlichen Gruppe \(G\). Analog ist \( |N| \) die Anzahl der Elemente in der normalen Untergruppe \(N\) von \(G\) (und damit die Elementanzahl in jeder Scheibe) und \( |G/N| \) die Anzahl der Elemente in der Faktorgruppe (also die Anzahl Scheiben). Dann gilt: \[ |G| = |N| \cdot |G/N| \] Dies ist auch die Motivation für die Schreibweise \( G/N \) für die Faktorgruppe. |
Man kann das obige Zerlegungsverfahren mehrfach wiederholen:
Wir gehen also schrittweise zu immer kleineren Gruppen \( N, N', N'', ... \) über, die jeweils normal bezüglich der vorhergehenden Untergruppe sind. Dabei wird jede Gruppe durch die nächste Gruppe in Scheiben zerlegt, d.h. es entstehen die Faktorgruppen \( G/N, \, N/N', \, N'/N'', \, ... \) .
Ist diese Zerlegung nun eindeutig, oder gibt es mehrere Möglichkeiten, eine Gruppe \(G\) wie oben schrittweise zu zerlegen? Immerhin gibt es ja oft mehr als eine normale Untergruppe, mit der man die Zerlegung weiterführen kann! Wenn man aber in jedem Schritt immer eine der möglichst großen (maximalen) normalen Untergruppen nimmt, so sagt das Jordan-Hölder-Theorem dazu folgendes:
|
Jordan-Hölder-Theorem: Zu jeder endlichen Gruppe \(G\) kann man mindestens eine Zerlegungsliste \[ G, N, N', N'', \, ... \, , 1 \] angeben, so dass folgendes gilt:
Man nennt eine solche Zerlegungsliste \( G, N, N', N'', \, ... \, , 1 \) auch eine Kompositionsreihe von \(G\). Es kann sein, dass es mehrere Kompositionsreihen zur selben Gruppe \(G\) gibt (so kann es in jedem Schritt mehrere maximale normale Untergruppen geben, die zur Zerlegung in Frage kommen). Insgesamt ist die Anzahl der Untergruppen in den verschiedenen Kompositionsreihen aber immer dieselbe, d.h. man kommt immer nach derselben Anzahl Schritte bei der trivialen Gruppe \(1\) an. Die Faktorgruppen, die bei den verschiedenen Kompositionsreihen entstehen, sind insgesamt für eine gegebene Gruppe \(G\) immer dieselben, wobei sie allerdings in unterschiedlicher Reihenfolge auftreten können (nicht jede denkbare Faktorgruppen-Reihenfolge muss dabei durch eine entsprechende Kompositionsreihe erzeugt werden). Damit ergibt sich aus jeder möglichen Kompositionsreihe dieselbe Sammlung einfacher Gruppen als Faktorgruppen, d.h. in diesem Sinne lässt sich jede endliche Gruppe in eindeutiger Weise in einfache Gruppen zerlegen.
|
Der Beweis dieses Theorems würde den Rahmen hier sprengen, auch wenn er nicht allzu
kompliziert ist.
Anschaulich sagt das Theorem: Man kann eine Gruppe in verschiedener Weise in kleinere Scheiben zerlegen:
erst Scheiben senkrecht schneiden, dann die entsprechende \(N\)-Scheibe quer in kleinere Scheiben schneiden usw..
Die Faktorgruppen-Strukturen, die dabei zwischen den Längs-Scheiben, den Quer-Scheiben etc. entstehen,
sind bei einer gegebenen Gruppe insgesamt immer dieselben, wenn man immer möglichst große Scheiben
(maximale normale Untergruppen) für das Zerschneiden nimmt.
Insbesondere sind die Faktorgruppen einfache Gruppen, d.h. man
kann sie nicht ihrerseits in kleinere Scheiben zerschneiden.
Wie wir von oben wissen, verliert man beim Zerschneiden Information. Daher kann man die Bausteine nicht ohne Zusatzwissen wieder zur Gesamtgruppe \(G\) zusammenfügen. Es bleibt die Hoffnung, dass nicht allzuviel Information verloren geht, so dass die Bausteine immer noch wesentliche Informationen über die Gruppe enthalten. Umgekehrt gilt aber in jedem Fall: Man muss die inneren Struktur der Bausteine kennen, um überhaupt eine Chance zu haben, die Struktur der daraus aufgebauten Gruppe \(G\) zu ergründen. Schauen wir uns also etwas genauer an, was man bisher über diese Bausteine (die einfachen Gruppen) herausgefunden hat.
Welche möglichen Baustein-Sorten (einfache Gruppen) gibt es? Seit etwa 1982 weiß man es, denn es ist vielen Mathematikern in einem enormen Kraftakt über einige Jahrzehnte hinweg gelungen, eine vollständige Übersicht (Klassifikation) über die einfachen Gruppen zu erstellen – wir hatten es oben bereits erwähnt. In Wikipedia: Endliche einfache Gruppe finden wir dazu die folgende Liste:
|
Die Klassifikation endlicher einfacher Gruppen:
|
Schauen wir uns an, was das jeweils bedeutet:
Das Wort abelsch bedeutet, dass in diesen Gruppen das Kommutativgesetz gilt,
d.h. \( a b = b a \). Das vereinfacht die möglichen Gruppenstrukturen erheblich.
So wissen wir von oben, dass dann jede Untergruppe
eine normale Untergruppe ist.
Eine abelsche Gruppe hatten wir oben bereits kennengelernt: \(\mathbb{Z}_N^*\)
(die multiplikative Gruppe modulo N).
Zur Erinnerung: Diese Gruppe besteht aus allen natürlichen Zahlen von \(1\) bis \(N\), die teilerfremd
zu \(N\) sind (wobei \(1\) als teilerfremd zu \(N\) zählt), und die Gruppenverknüpfung ist durch
\[
a \circ b := (a \cdot b) \;\mathrm{mod}\; N
\]
definiert, d.h.
die beiden Zahlen \(a\) und \(b\) werden miteinander multipliziert
und anschließend wird noch ein möglichst großes Vielfaches von \(N\) abgezogen.
Für \( N = 15 = 3 \cdot 5 \) sah die Gruppe so aus:
\[
\mathbb{Z}_{15}^* = \{ 1, 2, 4, 7, 8, 11, 13, 14 \}
\]
Wir hatten sie oben auch als Rad mit entsprechenden Speichen dargestellt.
Hier ist die Multiplikationstabelle für diese Gruppe, wobei ich versucht habe,
die einzelnen Untergruppen farbig darzustellen (graue Elemente gehören gleichzeitig zu mehreren
Untergruppen):
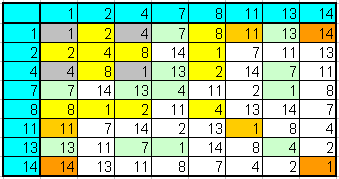
Es gibt insgesamt nur Untergruppen mit 2 und mit 4 Elementen (die triviale Gruppe lassen wir weg). Hier sind sie: \[ \{1, 4\} \] \[ \{1, 11\} \] \[ \{1, 14\} \] \[ \{1, 2, 4, 8\} \] \[ \{1, 7, 4, 13\} \] Wegen der Abgeschlossenheit muss bei einer Gruppe jede mehrfache Gruppenmultiplikation eines Gruppenelementes mit sich selbst (wir sagen Potenz) wieder in der Gruppe liegen. Das Besondere bei den obigen Untergruppen ist nun, dass man sich jeweils ein passendes Element (den sogenannten Generator) herausgreifen kann, so dass dessen Potenzen (bezüglich der Gruppenverknüpfung) alle anderen Untergruppenelemente ergeben.
Bei den Untergruppen mit nur 2 Elementen ist das schnell klar. So ist \(4\) der Generator der Untergruppe \( \{1, 4\} \) (in der Tabelle oben die grauen Kästchen), denn \begin{align} 4 \;\mathrm{mod}\; 15 &= 4 \\ 4^2 \;\mathrm{mod}\; 15 &= 1 \end{align}
Aber es gilt auch bei den beiden Untergruppen mit 4 Elementen. So kann man für die Untergruppe \( \{1, 2, 4, 8\} \)wahlweise die \(2\) oder die \(8\) als Generator nehmen, denn \begin{align} 1 &= 2^4 \;\mathrm{mod}\; 15 = 8^4 \;\mathrm{mod}\; 15 \\ 2 &= 2^1 \;\mathrm{mod}\; 15 = 8^3 \;\mathrm{mod}\; 15 \\ 4 &= 2^2 \;\mathrm{mod}\; 15 = 8^2 \;\mathrm{mod}\; 15 \\ 8 &= 2^3 \;\mathrm{mod}\; 15 = 8^1 \;\mathrm{mod}\; 15 \end{align} Für die Untergruppe \( \{1, 7, 4, 13\} \) kann man analog wahlweise die \(7\) oder die \(13\) als Generator nehmen.
Gruppen, die sich so darstellen lassen, nennt man zyklische Gruppen:
|
zyklische Gruppen:
Man bezeichnet eine Gruppe als zyklisch, wenn es mindestens ein Element \( a \) in der Gruppe gibt, so dass sich jedes Element \(g\) der Gruppe als \(k\)-faches Gruppenprodukt von \(a\) mit sich selbst schreiben lässt (mit jeweils passender natürlicher Zahl \(k\)): \begin{align} g &= a \circ a \circ \, ... \, \circ a = \\ &=: a a ... a =: a^k \end{align} (wobei wir in der Mitte das Gruppenverknüpfungszeichen \( \circ \) weggelassen und rechts die Potenzschreibweise als \(k\)-faches Gruppenprodukt zu verstehen ist). Umgekehrt muss auch jedes \(a^k\) mit beliebiger natürlicher Zahl \(k\) in der Gruppe liegen (denn \(a\) ist ja Element der Gruppe und die Gruppenmultiplikation mit \(a\) darf wegen der abgeschlossenheit nicht aus der Gruppe herausführen). Man bezeichnet das Element \(a\) auch als Generator der Gruppe. Es kann mehrere verschiedene Generatoren in einer Gruppe geben. Eine endliche zyklische Gruppe \(C_n\) mit \(n\) Elementen lässt sich insgesamt schreiben als \[ C_n = \{ a , a^2 , a^3 , \, .... , a^n \} \] mit \( a^n = 1 \). Zyklische Gruppen sind automatisch abelsch, d.h. die Gruppenelemente lassen sich miteinander vertauschen.
|
Die zyklischen Untergruppen von \( \mathbb{Z}_{15}^* \) kann man
auch sehr schön in einem Zyklen-Diagramm (engl.: cycle graph) darstellen:
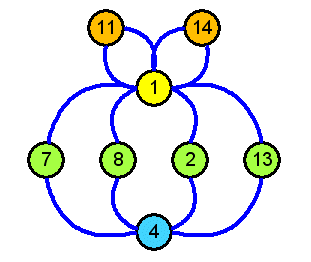
Oben sieht man die beiden Untergruppen mit je 2 Elementen, unten die beiden Untergruppen mit je 4 Elementen. Bewegt man sich im unteren äußeren Zyklus links herum, so entspricht jeder Schritt einer Multiplikation mit dem Generator 7 (modulo 15) und man überstreicht die Elemente 1, 7, 4, 13 . Läuft man den Zyklus in umgekehrter Richtung, so entspricht jeder Schritt einer Multiplikation mit dem Generator 13 (modulo 15).
Versuchen wir, unser obiges Zerlegungsverfahren anzuwenden und eine Kompositionsreihe für \( \mathbb{Z}_{15}^* \) aufzustellen, also die Gruppe in Scheiben zu zerschneiden. Dazu wählen wir im ersten Schritt eine möglichst große Untergruppe \(N\) aus, beispielsweise \[ N = \{1, 2, 4, 8\} \] Diese Gruppe ist automatisch normal, da unsere Ausgangsgruppe abelsch ist. Die anderen 4 Elemente von \( \mathbb{Z}_{15}^* \) liegen dann alle in der Menge \begin{align} 7 N &= \{7, 11, 13, 14\} = \\ &= \{ 7 \circ 1, \, 7 \circ 2, \, 7 \circ 4, \, 7 \circ 8 \} \end{align} Die Faktorgruppe \(\mathbb{Z}_{15}^*/N\) besteht dann aus diesen beiden Mengen (Scheiben) \( N \) und \( 7 N \) wobei \(N\) gleichsam die Scheibe mit Aufhängungspunkt \(1\) und \(7 N\) die Scheibe mit Aufhängungspunkt \(7\) ist. Das Gruppenprodukt in \(\mathbb{Z}_{15}^*/N\) ist dann so definiert (siehe oben): \begin{align} N \circ N &:= (1 \circ 1) N = N \\ N \circ (7 N) &:= (1 \circ 7) N = 7 N \\ (7 N) \circ N &:= (7 \circ 1) N = 7 N \\ (7 N) \circ (7 N) &:= (7 \circ 7) N = 4 N = N \end{align} Das bedeutet:
Das kann man sehr schön darstellen, wenn man in der Multiplikationstabelle die
Zeilen und Spalten vertauscht, so dass die Elemente von N und
7 N nacheinander kommen:
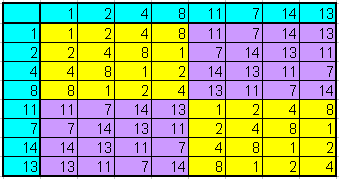
Plötzlich erkennt man die wirkliche Struktur der Gruppe \( \mathbb{Z}_{15}^* \):
Sie zerfällt in 4 Blöcke, wobei je zwei Blöcke identisch sind.
Aufgrund dieser Struktur könnte man folgende Übersetzung machen:
Setze \( a := 2 \) und \( b := 11 \) (auch \(b := 7\) wäre gegangen;
es ist ja \(7N = 11N\)).
Dann ist \(a\) Generator der Gruppe \( N = \{1, 2, 4, 8\} \) und
\(b\) ist Generator der Gruppe \( \{1, 11\} \),
die sich wie \(G/N\) verhält. Jedes Element g von \( \mathbb{Z}_{15}^* \)
lässt sich dann schreiben als
\[
g = a^p \, b^q
\]
(natürlich modulo 15)
mit \( p = 0, 1, 2, 3 \) und \( q = 0, 1 \).
Wir müssen nur noch wissen, dass \(a^4 = 1\) und
\(b^2 = 1\) ist (d.h. in Produkten dürfen vier a's und zwei b's immer
weggestrichen werden), um die komplette Gruppenmultiplikationstabelle
aufstellen zu können:
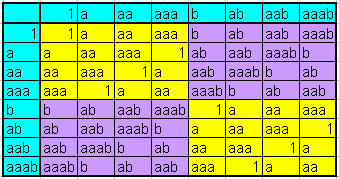
Mit den Bezeichnungen \begin{align} C_4 &:= \{1, a, aa, aaa\} \\ C_2 &:= \{1, b\} \end{align} für die beiden beteiligten zyklischen Gruppen schreibt man dann im obigen Sinn \[ \mathbb{Z}_{15}^* = C_4 \times C_2 \] und meint damit im Wesentlichen die obige Multiplikationstabelle. Etwas präziser bedeutet dieses sogenannte direkte Produkt zweier Gruppen \(G\) und \(G'\) folgendes:
|
direktes Produkt zweier Gruppen:
Aus zwei Gruppen \(G\) und \(G'\) kann man das direkte Produkt \( G \times G' \) bilden, indem man alle möglichen Paare \( (g,g') \) bildet (mit \(g \in G\) und \(g' \in G'\)) und die folgende Gruppenverknüpfung zwischen den Paaren definiert: \[ (g,g') \circ (h,h') := (g \circ h , g' \circ h') \] mit \(h \in G\) und \(h' \in G'\). Analog kann man auch das direkte Produkt von mehr als zwei Gruppen definieren.
|
Oben hatten wir einfach
\(\mathbb{Z}_{15}^* = C_4 \times C_2\)
geschrieben und mit der speziellen Wahl \(a = 2\) und \(b = 11\)
direkt die Zahlen von \(\mathbb{Z}_{15}^*\) durch \(a\) und \(b\) ausgedrückt.
Wir hätten aber auch andere Zahlen für \(a\) und \(b\) wählen können
(es gibt ja noch andere Generatoren
und auch andere zyklische Vierer- und Zweier-Untergruppen) – die Blockstruktur der Multiplikationstabelle
wäre bei passender Sortierung erhalten geblieben.
Mit dem gerade definierten direkten Gruppenprodukt kann man es noch etwas allgemeiner formulieren: Eigentlich brauchen wir für die obige Multiplikationstabelle der Produktgruppe \( C_4 \times C_2 \) gar keine Gruppenmultiplikation zwischen \(a\) und \(b\), denn statt beispielsweise \( aaab \) können wir darin auch \( (aaa , b) \) schreiben (allgemein also statt \( a^p \, b^q \) einfach \( (a^p , b^q) \). Zwischen diesen Paaren und den Elementen von \(\mathbb{Z}_{15}^*\) brauchen wir nun noch eine eindeutige (bijektive) Abbildung, die verträglich mit der Multiplikationstabelle oben ist (das nennt man einen Gruppen-Isomorphismus). Das bedeutet, dass man die Paare als Indices für die Gruppenelemente verwenden kann, also beispielsweise \( g_{(aaa , b)}\) schreiben kann, und dass das Gruppenverhalten der Indices das der Gruppe wiedergibt, beispielsweise so: \[ g_{(aaa , b)} \circ g_{(aa , b)} = g_{(aaaaa , bb)} = g_{(a , 1)} \] denn \(a^4 = 1\) und \(b^2 = 1\) (siehe oben). In diesem Sinne sagt man auch, dass die Gruppe \(\mathbb{Z}_{15}^*\) isomorph zur Produktgruppe \( C_4 \times C_2 \) ist, denn die Elemente lassen sich eins-zu-eins einander zuordnen, so dass die Multiplikationstabelle von \( C_4 \times C_2 \) diejenige von \(\mathbb{Z}_{15}^*\) ergibt und umgekehrt.
Die endliche abelsche Gruppe \(\mathbb{Z}_{15}^*\) ist also isomorph zum direkten Produkt zweier zyklischer Gruppen. Ganz allgemein kann man zeigen, dass für endliche abelsche Gruppen analog folgendes gilt:
|
Hauptsatz über endliche abelsche Gruppen:
Jede endliche abelsche Gruppe \(G\) ist isomorph zu einem direkten Produkt endlich vieler zyklischer Gruppen: \[ G \cong C_{n_1} \times C_{n_2} \times \, ... \, \times C_{n_k} \] (das Zeichen \(\cong\) bedeutet "ist isomorph"; \(k\) darf auch \(1\) sein). Dabei sind die Elementzahlen \( n_1, n_2, \, ... , n_k \) der zyklischen Gruppen jeweils Primzahlen oder Potenzen von Primzahlen, die (bis auf die Reihenfolge) eindeutig durch \(G\) bestimmt sind (wobei durchaus auch zweimal dieselbe Zahl auftreten darf).
|
Als Beispiel hatten wir oben
\[
\mathbb{Z}_{15}^* \cong C_4 \times C_2
\]
gefunden,
d.h.die Primzahl-Potenzen \( 2^1 = 2 \)
und \( 2^2 = 4 \) treten hier auf.
Wie die Gruppen \(\mathbb{Z}_N^*\) für andere N
als Produkt zyklischer Gruppen aussehen, findet
man in
Wolfram MathWorld: Modulo Multiplication Group.
So ist beispielsweise
\begin{align}
\mathbb{Z}_{5}^* &\cong C_4 \\
\mathbb{Z}_{8}^* &\cong C_2 \times C_2 \\
\mathbb{Z}_{10}^* &\cong C_4 \\
\mathbb{Z}_{12}^* &\cong C_2 \times C_2 \\
\mathbb{Z}_{21}^* &\cong C_2 \times C_6 \\
& ...
\end{align}
Wenn man passende Zahlen für die Elemente \(a\), \(b\) etc. der zyklischen Gruppen
einsetzt, kann man auch \(=\) (gleich) statt \(\cong\) (isomorph) schreiben.
Die Gruppen \(\mathbb{Z}_N^*\) können also für verschiedene \(N\)
durchaus gleichwertige Multiplikationstabellen aufweisen (also isomorph zueinander sein).
Übrigens werden wir gleich noch sehen, dass \( C_4 \)
nicht isomorph zu \( C_2 \times C_2 \) ist, auch wenn
\(C_2\) eine Untergruppe von \(C_4\) ist.
Wie kommt man darauf, dass für die Elementzahlen der zyklischen Gruppen die Potenz einer Primzahl ausreicht? Das liegt daran, dass man diese zyklischen Gruppen nicht als direktes Produkt kleinerer zyklischer Gruppen schreiben kann. Sie bilden also die kleinsten Bausteine, wenn man eine abelsche Gruppe als direktes Produkt schreiben möchte. Generell kann man eine zyklische Gruppe \(C_n\) nämlich genau dann als Produkt \( C_n = C_p \times C_q \) schreiben, wenn \( n = p q \) ist und zusätzlich \(p\) und \(q\) teilerfremd (also auch verschieden) sind (Begründung folgt gleich).
Wenn aber nun \(n\) eine Primzahl oder Potenz einer Primzahl ist, dann lässt sich \(n\) nicht in teilerfremde verschiedene Faktoren \(p\) und \(q\) aufteilen. Entsprechend lässt sich \(C_n\) auch nicht als Produkt kleinerer zyklischer Gruppen schreiben. So lässt sich beispielsweise \(C_4\) nicht als \( C_2 \times C_2 \) schreiben, denn in \(C_4\) muss man ein Element viermal mit sich selbst multiplizieren, um \(1\) zu erhalten, in \( C_2 \times C_2 \) dagegen reicht zweimal.
Hier nun die versprochene Begründung: Wir bilden das direkte Produkt \[ C_p \times C_q \] \begin{align} C_p &= \{a, a^2, \, ... \, , a^p=1 \} \\ C_q &= \{b, b^2, \, ... \, , b^q=1 \} \end{align} Nun suchen wir die kleinste Zahl \(n\), für die \( (a,b)^n = 1 \) ist, d.h. \( (a^n,b^n) = (1,1) \) und somit \( a^n = 1 \) und \( b^n = 1 \). Wir wissen, dass \(p\) und \(q\) die kleinsten Zahlen sind, so dass \( a^p = 1 \) und \( b^q = 1 \) ist, d.h. \(n\) muss das kleinste gemeinsame Vielfache von \(p\) und \(q\) sein. Da \(p\) und \(q\) teilerfremd sein sollen, ist ihr kleinstes gemeinsames Vielfaches gleich ihrem Produkt \(p \cdot q \), d.h. wir haben \(n = pq\).
Die Gruppe \( C_p \times C_q \) enthält also mindestens die folgenden \(n = pq\) verschiedene Elemente: \[ \{ (a,b), (a,b)^2, \, ... \, , (a,b)^n \} \] mit \( (a,b)^n = (a^n,b^n) = 1 = (1,1) \). Andererseits enthält sie als Produktgruppe sowieso nur \(pq\) Elemente (nämlich jedes der \(p\) Elemente von \(C_p\) mit jedem der \(q\) Elemente von \(C_q\) als Paar kombiniert). Also umfasst die obige Liste der Potenzen von \( (a,b) \) bereits alle Elemente von \(C_p \times C_q\) , d.h. diese Gruppe ist zyklisch mit Generator \( (a,b) \) und \( n = p q \) Elementen. Insgesamt ist also \[ C_n = C_p \times C_q = \] \[ = \{ (a,b), (a,b)^2, \, ... \, , (a,b)^n \} \] wenn \( n = p q \) ist und zusätzlich \(p\) und \(q\) teilerfremd (und damit auch verschieden) sind.
Endliche abelsche Gruppen sind also nach dem obigen Hauptsatz von ihrer Gruppenstruktur her gleichwertig zu direkten Produkten zyklischer Gruppen \(C_n\), wobei \(n\) eine Primzahl oder Primzahlpotenz ist. Damit hat man eine vollständige Übersicht über alle abelschen Gruppen. Diese Produktstruktur ist allerdings nicht unbedingt identisch mit der Zerlegung in einfache Gruppen nach dem Jordan-Hölder-Theorem von oben, denn die zyklischen Gruppen \(C_n\) sind nur dann einfache Gruppen, wenn \(n\) eine Primzahl ist (aber keine höhere Potenz einer Primzahl).
Begründung: Wenn \(n\) sich als Produkt zweier (nicht unbedingt teilerfremder) Zahlen \(p\) und \(q\) schreiben lässt, so umfasst die von \(a\) generierte zyklische Gruppe \(C_n\) die zyklische Untergruppe \(C_p\) (mit Generator \(b := a^q\)) und umgekehrt (mit \(p\) und \(q\) vertauscht). Die Gruppe \( C_4 = \{1, a, a^2, a^3 \} \) enthält beispielsweise die Untergruppe \( C_2 = \{1, a^2\}\), auch wenn sie sich nicht als Produkt mit dieser Gruppe schreiben lässt. Das zeigt sehr schön, dass man eine Gruppe \(G\) mit Hilfe einer normalen Untergruppe \(N\) zwar in \(N\) und \(G/N\) zerlegen kann, aber trotzdem nicht \( G = N \times (G/N) \) sein muss.
Wenn \(n\) bei \(C_n\) dagegen eine Primzahl ist, dann hat \(C_n\) keine echten Untergruppen, d.h. \(C_n\) ist eine endliche einfache abelsche Gruppe.
Umgekehrt kann man sich überlegen, dass jede abelsche Gruppe \(G\) mit \(n\) Elementen und \(n\) einer Primzahl zyklisch sein muss (und damit einfach ist). Das folgt direkt aus der Darstellung als direktes Produkt zyklischer Gruppen, denn in diesem Fall hat dieses Produkt nur einen Faktor, nämlich \( G = C_n \).
Man kann diese Aussage aber auch sehr leicht direkt mit dem Satz von Lagrange (siehe oben) beweisen: Nehmen wir ein Element \(g\) (ungleich \(1\)) aus der Gruppe heraus und betrachten die zyklische Untergruppe, die von \(g\) generiert wird, also die Untergruppe \( U = \{1, g, g^2, ... \} \). Die Anzahl Elemente in \(U\) muss nach dem Satz von Lagrange ein Teiler von \(n\) sein, und da \(n\) eine Primzahl ist, muss sie gleich \(n\) sein, d.h. \(U\) hat genausoviele Elemente wie \(G\) und ist damit gleich \(G\). Also kann \(G\) als zyklische Gruppe \( G = \{1, g, g^2, ... \} \) geschrieben werden, wobei \(g\) ein beliebiges Element aus \(G\) (ungleich \(1\)) sein kann.
Damit haben wir die kleinsten Bausteine der endlichen abelschen Gruppen im Sinne des Jordan-Hölder-Theorems gefunden, nämlich die endlichen abelschen einfachen Gruppen, die identisch sind mit den zyklischen Gruppen von Primzahlordnung:
|
Die endlichen einfachen abelschen Gruppen: Die endlichen einfachen abelschen Gruppen sind genau die abelschen Gruppen, deren Elementanzahl \(n\) eine Primzahl ist (man spricht von einer abelschen Gruppe von Primzahlordnung). Diese Gruppen sind zugleich zyklisch, also isomorph zu den Gruppen \(C_n\) (wobei \(n\) eine Primzahl ist).
|
Wenn man als Nicht-Fachmann nach einer Definition für Gruppen vom Lie-Typ sucht, dann findet man meist nur Beispiele, aber nur selten echte Definitionen, und die sehen auf den ersten Blick recht unverständlich aus. So fand man vor einigen Jahren in Wikipedia: Group of Lie type:
Etwas verständlicher ist die folgende Umschreibung in Wolfram MathWorld: Lie-Type Group:
A Lie group is a group with the structure of a manifold. Therefore, discrete groups do not count. However, the most useful Lie groups are defined as subgroups of some matrix group. The analogous subgroups where the matrices are taken to be over a finite field (but the group is defined in the same way) are called the Lie-type groups. They are a kind of linear algebraic group.
Was bedeutet das? Was Lie-Gruppen üblicherweise sind, ist relativ einfach anschaulich erklärt: Die Gruppenelemente hängen kontinuierlich von endlich vielen reellen Parametern ab. Ein Beispiel sind die Drehungen im dreidimensionalen Raum. Jede Drehung hängt kontinuierlich von Drehachse und Drehwinkel ab (siehe Die Symmetrie der Naturgesetze, Kapitel 4.8 ). Die Drehungen bilden daher insgesamt eine sogenannte Mannigfaltigkeit, also einen kontinuierlichen (hier dreidimensionalen) Raum, in dem die Gruppenparameter (z.B. Drehwinkel) als Koordination verwendet werden können und in dem jeder Punkt ein Gruppenelement darstellt. Man kann auch sehr kleine Änderungen der Gruppenparameter betrachten und so beispielsweise sehr kleine (infinitesimale) Drehungen definieren. Das führt dann zum Begriff der sogenannten Lie-Algebra.
Bei den Drehungen (und den meisten anderen Lie-Gruppen) kann man die Gruppenelemente durch passende Matrizen darstellen, beispielsweise durch SO(3) -Matrizen. Die SO(3) -Matrizen stellen lineare Abbildungen im dreidimensionalen Raum dar, die keine Längen ändern und die keine Spiegelungen enthalten – die also anschaulich Drehungen sind. Die SO(3)-Matrizen bilden eine sogenannte Matrixgruppe. Auch die meisten anderen Lie-Gruppen lassen sich durch passende Matrixgruppen darstellen, wobei die Matrixelemente kontinuierlich von den Gruppenparametern abhängen.
Wenn man nun keine kontinuierlichen Matrixelemente mehr zulässt, sondern nur noch endlich viele verschiedene Werte erlaubt sind, dann wird aus der kontinuierlichen Lie-Gruppe eine Gruppe vom Lie-Typ. Man könnte beispielsweise die Drehungen im Raum so einschränken, dass nur noch die drei Drehachsen in x- , y- oder z-Richtung erlaubt sind sowie Drehwinkel, die Vielfache von 90 Grad sind. Das entspricht genau den Drehungen, die einen Würfel unverändert lassen. Man sagt daher auch oft, Gruppen vom Lie-Typ sind Matrix-artige endliche Gruppen, die bestimmte geometrische Objekte invariant lassen.
Natürlich muss man aufpassen, dass man bei der Einschränkung von kontinuierlichen auf endlich viele Werte für die Matrixelemente die Gruppenstruktur sowie die Zusatzbedingungen, die auch die kontinuierlichen Matrizen der Matrixgruppe erfüllen müssen, nicht zerstört. Mathematisch müssen die endlich vielen Werte der Matrixelemente daher aus einem sogenannten endlichen Körper (engl.: finite field) stammen, so dass bei der Matrixmultiplikation die Addition und Multiplikation der Matrixelemente immer nur wieder erlaubte Matrixelemente ergibt und so dass die Gruppeneigenschaften für die Matrizen erfüllt bleiben (mehr dazu weiter unten).
Die untere der beiden Definitionen haben wir damit soweit verstanden, bis auf den Hinweis, dass Gruppen vom Lie-Typ zu den linearen algebraischen Gruppen gehören. In Wikipedia: Linear algebraic group findet man, dass damit tatsächlich ausschließlich Matrixgruppen gemeint sind, also Untergruppen der invertierbare n-mal-n-Matrizen. Kontinuierliche Lie-Gruppe, die nicht durch Matrixgruppen dargestellt werden können, spielen also als Ausgangspunkt für unsere endlichen Gruppen vom Lie-Typ keine Rolle. Wir haben es ausschließlich mit Matrizen zu tun! Welche Matrizen zur gewünschten Matrixgruppe gehören, wird dabei durch Zusatzbedingungen festgelegt, die diese Matrizen erfüllen müssen. Das Wort algebraisch erklärt sich nun dadurch, dass diese Zusatzbedingungen durch polynomiale Gleichungen für die Matrixelemente gegeben sein müssen.
Können wir mit diesem Vorwissen nun auch die obere Definition verstehen? Dort ist von einer group of rational points die Rede. In Wikipedia: Rational point findet man dazu, dass die Koordinaten der rationalen Punkte (also hier die Matrixelemente) nur Werte aus dem endlichen Körper annehmen können – das kennen wir schon! Zum Wort reductive findet man in Wikipedia: Reductive group eine komplizierte Beschreibung, und wenn man zu Wikipedia: Unipotent weitergeht, dann wird klar, dass man es mit einer Zusatzforderung für bestimmte normale Untergruppen zu tun hat. Da wir uns aber nur für einfache Gruppen interessieren, spielt das keine Rolle, denn diese enthalten sowieso keine nicht-trivialen normalen Untergruppen. Vergessen wir also dieses hier irrelevante technische Detail. Wir halten also fest:
|
Endliche einfache Gruppen vom Lie-Typ: Diese Gruppen lassen sich durch invertierbare n-mal-n -Matrizen darstellen, bei denen die Matrixelemente nur bestimmte endlich viele Werte annehmen können. Diese Werte müssen aus einem sogenannten endlichen Körper stammen, damit die Matrixmultiplikation die Gruppenaxiome erfüllen kann. Zusätzlich können polynomiale Gleichungen für die Matrixelemente die erlaubten Werte weiter einschränken. Da die Gruppen einfach sein sollen, dürfen sie keine echten nichttrivialen normalen Untergruppen enthalten.
|
endliche Körper:
Wenn man Matrizen miteinander multipliziert, so werden die Matrixelemente der entsprechenden Zeilen und Spalten miteinander multipliziert und diese Produkte dann aufaddiert, um die Matrixelemente der Produktmatrix zu berechnen. Bei den Matrizen einer endlichen Gruppe muss diese Produktmatrix natürlich wieder zu der betrachteten Matrixgruppe gehören (Abgeschlossenheit der Gruppe), d.h. ihre Matrixelemente müssen wieder einen der endlich vielen Werte annehmen, aus dem alle Matrixelemente der endlichen Gruppe stammen sollen. Addition und Multiplikation dürfen also nicht aus diesem endlichen Wertebereich hinausführen. Außerdem müssen dieselben Rechenregeln gelten, wie man sie von reellen Zahlen gewohnt ist, denn nur so erfüllt die Matrixmultiplikation die Regeln für eine Gruppenverknüpfung (beispielsweise das Assoziativgesetz). Schaut man sich die Details an, so findet man, dass die Matrixelemente und ihre Additions- bzw. Multiplikationsverknüpfung insgesamt die Regeln eines sogenannten endlichen Körpers erfüllen müssen. Genauer bedeutet das:
|
Definition eines endlichen Körpers:
Man benötigt eine endliche Menge sowie zwei Verknüpfungen \(+\) und \(\cdot\) zwischen den Elementen dieser Menge (wir nennen sie Addition und Multiplikation), wobei die folgenden Gesetze gelten:
|
Das sind genau die Gesetze, wie sie auch für das Rechnen mit reellen Zahlen gelten.
In einem endlichen Körper können wir also formal wie mit Zahlen rechnen, wobei die
Addition und die Multiplikation aber so gestaltet sein müssen, dass der endliche Zahlenbereich
nicht verlassen wird. Wie man das erreichen kann, haben wir oben bei der
multiplikativen Gruppe modulo \(N\), also \(\mathbb{Z}_N^*\)
gesehen: Man rechnet wie auf einem Rad, zieht also vom Ergebnis immer ein
möglichst großes Vielfaches von \(N\) ab.
Das kann man auch für die Addition so machen und so versuchen,
aus \(\mathbb{Z}_N^*\) durch Hinzunahme der Addition modulo \(N\)
einen endlichen Körper zu machen. Das funktioniert aber nur dann, wenn im Rad keine Speichen
fehlen, wenn also \(\mathbb{Z}_N^*\) keine Lücken hat.
Schließlich muss eine Addition von \(1\) (modulo \(N\)), also ein Schritt rechts herum auf dem Rad
immer möglich sein. Im Rad fehlen aber generell alle Speichennummern, die einengemeinsamen Teiler mit
der Speichenanzahl \(N\) haben. Deshalb muss hier \(N\) eine Primzahl sein, denn
dann können alle Speichen drin bleiben.
Die Menge der Zahlen von \( 0 \) bis \( N - 1 \) bildet also zusammen mit
der Addition und Multiplikation (beides modulo \(N\)) einen endlichen Körper, wenn \(N\) eine Primzahl ist.
Statt \(N\) schreiben wir dann auch \(p\) für die Primzahl und entsprechend
\(\mathbb{Z}_p^{(*,+)}\)
für den zugehörigen endlichen Körper.
|
Man kann zeigen, dass jeder Körper mit \(p\) Elementen (wobei \(p\) eine Primzahl ist)
isomorph zu \(\mathbb{Z}_p^{(*,+)}\) ist,
d.h. die komplette Additions- und Multiplikationstabelle jedes Körpers mit \(p\) Elementen
lässt sich durch geeignete Umbenennung der Elemente in die Tabellen von
Zp(*,+) übersetzen.
Umgekehrt gibt es zu jeder Primzahl \(p\) auch einen endlichen Körper mit \(p\) Elementen.
Welche anderen endlichen Körper gibt es? Man kann zeigen, dass die Elementanzahl immer die Potenz einer Primzahl \(p\) (der sogenannten Charakteristik des Körpers) sein muss, und dass es umgekehrt auch zu jeder Primzahlpotenz \(p^n\) einen entsprechenden endlichen Körper gibt, der bis auf Isomorphie eindeutig ist. Die Elemente eines solchen Körpers schreibt man am einfachsten in Form von Polynomen mit Koeffinzienten aus \(\mathbb{Z}_p^{(*,+)}\). Diese Polynome kann man addieren und multiplizieren, wobei für die Koeffinzienten immer modulo \(p\) gerechnet werden muss, denn sie sollen ja aus \(\mathbb{Z}_p^{(*,+)}\) stammen. Allerdings muss man noch sicherstellen, dass es ein inverses Element (Polynom) für die Multiplikation gibt und dass durch Multiplikation nicht Polynome mit zu großen Potenzen von \(x\) entstehen (der Körper soll ja endlich sein). Dazu braucht man ein sogenanntes irreduzibles Polynom, also ein Polynom \(F(x)\), das sich nicht als Produkt zweier anderer Polynome schreiben lässt (wobei die Polynome nicht einfach Zahlen aus \(\mathbb{Z}_p^{(*,+)}\) sein sollen; zu beachten ist, dass beim Produkt immer modulo \(p\) für die Koeffizienten gerechnet werden muss). Dieses irreduzible Polynom ist das Analogon zur obigen Primzahl \(p\). Entsprechend definiert man das Produkt zweier Polynome immer modulo des irreduziblen Polynoms \(F(x)\), d.h. man zieht vom Produkt immer ein möglichst großes Vielfaches von \(F(x)\) ab.
Die Polynomdarstellung der Elemente dient nur dazu, die Multiplikation der Elemente übersichtlich durch die Multiplikation von Polynomen (modulo \(F(x)\)) darzustellen. Man kann alternativ aber auch die Koeffizienten der einzelnen Potenzen von \(x\) des Polynoms einfach als Vektor schreiben, also statt \( 1 + 2x + 4x^2 \) die Schreibweise \( (1, 2, 4) \) verwenden. Die Addition der Körperelemente entspricht dann der Addition von Vektoren. Die Multiplikation ist dann aber nicht ganz so einfach abzulesen, denn dafür muss man die Polynommultiplikation modulo \(F(x)\) entsprechend in die Vektorschreibweise übersetzen.
Das irreduzible Polynom ist übrigens (analog zur Prinzahl \(p\)) selbst kein Element des Körpers, sondern der Körper besteht aus allen Polynomen mit einem Grad echt kleiner als der des irreduziblen Polynoms. Wenn \(F(x)\) also Grad 3 hat, dann besteht der Körper aus allen Polynomen der Form \( a x^2 + b x + c \) mit \(a, b, c \in \mathbb{Z}_p^{(*,+)}\). In Vektorschreibweise sind das alle Vektoren \( (a, b, c) \) mit \(a, b, c \in \mathbb{Z}_p^{(*,+)}\). Da \(\mathbb{Z}_p^{(*,+)}\) \(p\) Elemente besitzt, enthält dieser Körper \(p^3\) Elemente. Analog entstehen die anderen Körper mit \(p^n\) Elementen durch Wahl entsprechender irreduzibler Polynome \(F(x)\) vom Grad \(n\).
Hier ein Beispiel (siehe Wikipedia: Endlicher Körper ): Für \( p = 2 \) besteht \(\mathbb{Z}_2^{(*,+)}\) aus den Zahlen \( 0 \) und \( 1 \) und alle Rechnungen erfolgen modulo \(2\). Das irreduzible Polynom vom Grad \( n = 2 \) über diesem Koeffizienten-Körper ist \( F(x) = x^2 + x + 1 \). Der entsprechende Körper mit \( p^n = 2^2 = 4 \) Elementen besteht aus den Polynomen \( 0 , 1 , x , x + 1 \). Für \( n = 3 \) lautet das irreduzible Polynom über diesem Koeffizienten-Körper dagegen \( F(x) = x^3 + x + 1 \) und es ergeben sich 8 Polynome vom Grad 2 als Elemente des Körpers.
|
Die Struktur endlicher Körper: Jeder endliche Körper hat eine Anzahl Elemente, die durch die \(n\)-te Potenz einer Primzahl \(p\) gegeben ist (also \(p^n\)), und umgekehrt gibt es zu jeder Primzahl \(p\) und jeder natürlichen Zahl \(n\) einen solchen endlichen Körper mit \(p^n\) Elementen. Man nennt die Primzahl \(p\) auch Charakteristik des Körpers. Für \(n = 1\) ist dieser Körper isomorph zu \(\mathbb{Z}_p^{(*,+)}\) (siehe oben). Für größere \(n\) ist der Körper isomorph zur Menge der Polynome vom Grad kleiner als \(n\) mit Koeffizienten aus \(\mathbb{Z}_p^{(*,+)}\). Die Addition in diesem Körper entspricht der Polynomaddition, wobei die Koeffizienten modulo \(p\) addiert werden. Die Multiplikation entspricht der Polynommultiplikation, wobei die Koeffizienten modulo \(p\) multipliziert werden und am Schluss modulo \(F(x)\) gerechnet wird. Dabei ist \(F(x)\) ein irreduzibles Polynom vom Grad \(n\), d.h. \(F(x)\) kann nicht als Polynomprodukt (modulo \(p\) für die Koeffizienten) von Polynomen mit kleinerem Grad geschrieben werden. Man kann die Koeffizienten jedes Polynoms \( a_1 + a_2 x + \, ... \, + a_n x^{n-1} \) auch als \(n\)-dimensionalen Vektor \( (a_1, a_2, \, ... \, , a_n) \) schreiben mit \( a_i \in \mathbb{Z}_p^{(*,+)}\). Jedes Körperelement entspricht dann einem solchen Vektor, d.h. der Körper ist zugleich ein \(n\)-dimensionaler Vektorraum über \(\mathbb{Z}_p^{(*,+)}\), wobei zusätzlich eine Multiplikation der Vektoren über die entsprechende Polynommultiplikation (siehe oben) definiert ist.
|
Damit ist jetzt auch endlich im Detail klar, was eine endliche Gruppe vom Lie-Typ ist:
Es handelt sich um invertierbare Matrizen, wobei die Matrixelemente durch passende
ganzzahlige Polynome dargestellt werden können und die Addition / Multiplikation dieser Polynome
modulo \(p\) bzw. modulo \(F(x)\) gerechnet wird. Schauen wir uns nun einige Beispiele
für endliche Gruppen vom Lie-Typ an
(siehe Wikipedia: Group of Lie type ):
klassische Lie-Gruppen:
Dieser Begriff ist historisch zu verstehen – es handelt sich hier um lange bekannte und oft verwendete Lie-Gruppen. Hier einige Beispiele:
Um endliche Gruppen zu erhalten müssen wir natürlich die kontinuierlichen Matrixelemente wieder durch Elemente eines Körpers ersetzen, wobei die Matrizen dieselben Nebenbedingungen erfüllen müssen wir ihre kontinuierlichen Gegenstücke.
Chevalley-, Steinberg- und Suzuki-Ree-Gruppen:
Bei den kontinuierlichen Lie-Gruppen kennt man den Begriff der Lie-Algebra. Man erhält diese Lie-Algebra, indem man die Gruppenelemente in infinitesimaler Nähe des neutralen Gruppenelementes 1 betrachtet. Umgekehrt bestimmt dann die Lie-Algebra auch die Struktur der Gruppe in einer gewissen Umgebung des 1-Elementes. Allerdings kann es durchaus verschiedene Gruppen mit derselben Lie-Algebra geben, beispielsweise die Gruppen \(\mathrm{SO}(3)\) und \(\mathrm{SU}(2)\).
Man kann nun auch bei endlichen Gruppen von Lie-Algebren ausgehen und Rezepte entwickeln, um systematisch zugehörige endliche Gruppen zu konstruieren. Ein solches Rezept hat Claude Chevalley Mitte der 50er-Jahre für beliebige endliche Körper entwickelt und so die Chevalley-Gruppen konstruiert, die auch viele klassichen Gruppen (siehe oben) beinhalten. Allerdings konnte er beispielsweise die unitären Matrizen so nicht erzeugen. Daher änderte Steinberg dieses Rezept geeignet ab und konnte so weitere endliche Gruppen erzeugen. Weitere endliche Matrixgruppen konnten 1960 von Michio Suzuki gefunden werden, indem er Steinbergs Rezept für bestimmte Spezialfälle abwandelte.
Um die alternierenden Gruppen zu verstehen, starten wir mit einer sehr allgemeinen Sorte von endlichen Gruppen: den Symmetrischen Gruppen. Eine Symmetrische Gruppe \(S_n\) ist dabei die Gruppe aller Vertauschungen (Permutationen), die bei \(n\) gegebenen Objekten möglich sind. Ein Beispiel: Bei 3 Objekten, die wir von 1 bis 3 durchnummerieren, könnte man beispielsweise \( (3, 1, 2) \) für eine Vertauschung dieser Objekte schreiben. Das bedeutet: Objekt Nummer 1 befindet sich jetzt da, wo vorher Objekt Nummer 2 war, Objekt Nummer 2 ersetzt Objekt Nummer 3 und Objekt 3 ersetzt Objekt 1. Man kann sich leicht überlegen, dass bei \(n\) Objekten \( n! = n \cdot (n - 1) \cdot (n - 2) \cdot ... \cdot 2 \cdot 1 \) verschiedene Vertauschungen dieser Objekte möglich sind, d.h. die Symmetrische Gruppe \(S_n\) hat \(n!\) (sprich: \(n\)-Fakultät) viele Elemente.
Bei größeren \(n\) wächst die Zahl der Elemente von \(S_n\) sehr rasch an, und es ergeben sich sehr viele komplexe Untergruppen. Tatsächlich gilt sogar:
Satz von Cayley:
|
Man kann sich also auch jede endliche Gruppe aus diesem Kapitel als eine Untergruppe von Vertauschungen vorstellen. Bei Rubiks Zauberwürfel ist das beispielsweise ganz offensichtlich, denn dort werden ja Ecken- und Kantensteine des Würfels vertauscht.
Die obige Vertauschung \( (3, 1, 2) \) können wir dadurch erreichen, dass wir erst die ersten beiden Objekte vertauschen (dann haben wir \( (2, 1, 3) \) ) und anschließend das erste und das letzte Objekt vertauschen (dann haben wir \( (3, 1, 2) \) ). Allgemein kann man jede Vertauschung durch mehrere Zweier-Vertauschungen (Transpositionen) ersetzen. Dabei steht eindeutig fest, ob man eine gerade oder eine ungerade Anzahl von Transpositionen benötigt. Entsprechend spricht man von geraden oder ungeraden Permutationen.
Führt man zwei gerade Permutationen nacheinander aus (man sagt, dass man sie multipliziert), so ist das Ergebnis wieder eine gerade Permutation, denn zwei gerade Anzahlen von Transpositionen ergeben zusammen wieder eine gerade Anzahl Transpositionen. Die geraden Permutationen bilden also eine Untergruppe der symmetrischen Gruppe. Das ist genau die alternierende Gruppe \(A_n\), um die es hier geht.
|
Die alternierende Gruppe \(A_n\) Die alternierende Gruppe \(A_n\) ist die Gruppe aller geraden Permutationen von \(n\) Objekten, d.h. jede Permutation der Gruppe lässt sich durch eine gerade Anzahl von Transpositionen (Zweier-Vertauschungen) ersetzen.
|
Die ungeraden Permutationen ergeben zusammen dagegen keine Untergruppe, denn führt man zwei ungerade Permutationen nacheinander aus, so ergibt das insgesamt eine gerade Permutation (denn die Summe zweier ungerader Zahlen ist eine gerade Zahl).
Die alternierende Gruppe \(A_n\) ist sogar eine normale Untergruppe (Normalteiler) von \(S_n\) (und zwar bis auf den Sonderfall \(n = 4\) sogar die einzige, siehe Wikipedia: Symmetrische Gruppe ). Wenn man nämlich aus einer geraden Permutation \(n \in A_n \) (hier als Name einer Permutation zu lesen) und irgendeiner anderen Permutation \(g\) das Gruppenprodukt \( g n g^{-1} \) bildet, so ergibt sich immer insgesamt wieder eine gerade Permutation, denn die Summe einer geraden Zahl mit zwei anderen Zahlen, die beide gerade oder ungerade sind, ergibt eine gerade Zahl. Für \( n > 4 \) ist \(A_n\) einfach, enthält also selber keine normale echte Untergruppe.
Was aber ist mit den Werten \(n = 1, 2, 3, 4\)?
Man könnte meinen, die bisherigen Gruppen müssten doch eigentlich alle endlichen einfachen Gruppen umfassen, die möglich sind. Speziell die Gruppen vom Lie-Typ mit ihren 16 jeweils unendliche Serien sind sehr vielfältig.
Und dennoch stellte sich im Lauf der Zeit heraus, dass es einzelne endliche einfache Gruppen gibt, die nicht in unsere bisherigen Schemata passen. Diese sporadischen Gruppen, wie man sie nennt, tauchen wie einsame Inseln aus dem Meer der bisherigen Gruppen auf. Sie definieren dabei keine Gruppen-Familien, die unendlich viele Mitglieder mit einer wachsenden Zahl von Elementen enthalten. Stattdessen haben sie jeweils eine genau festliegende Anzahl an Elementen.
Die ersten 5 dieser sporadischen Gruppen entdeckte der französische Mathematiker Émile Mathieu bereits in den Jahren 1862 und 1873 – man nennt sie nicht ganz überraschend Mathieu-Gruppen. Ab 1964 wurden dann nach und nach alle weitere sporadische Gruppen entdeckt – insgesamt sind es 26. Mehr dieser Inseln scheint es nicht zu geben, da ist man sich heute ziemlich sicher.
Was verbirgt sich hinter diesen Gruppen? Das ist leider nicht ganz einfach zu verstehen. Was aber auffällt: Immer wieder spiegeln die sporadischen Gruppen Symmetrien von gewissen endlichen mathematischen Strukturen wider. Man kann irgendetwas in diesen Strukturen vertauschen, ohne das Wesen der Struktur zu ändern. Das kennen wir bereits vom Zauberwürfel: Die Drehungen der einzelnen Würfelebenen vertauschen zwar Ecken und Kanten, aber es bleibt ein Würfel.
Dass es um Vertauschungen geht, überrascht uns nicht. Schließlich wissen wir von oben (Satz von Cayley), dass sich jede endliche Gruppe als Untergruppe der Symmetrische Gruppe \(S_n\) aller Vertauschungen von \(n\) Objekten schreiben lässt. Man braucht nur noch die passende Objektzahl \(n\) und eine Bedingung für die Auswahl der Untergruppe. Beides liefert die mathematische Struktur (z.B. der Würfel), deren Vertauschungs-Symmetrie durch die Gruppe beschrieben wird.
Bei den 5 Mathieu-Gruppen \(\mathbb{M}_{11}, \mathbb{M}_{12}, \mathbb{M}_{22}, \mathbb{M}_{23}, \mathbb{M}_{24}\) sind diese mathematischen Strukturen die sogenannten Wittschen Blockpläne, wobei die tiefergestellte Zahl dessen Punktzahl angibt. Diese Punkte des Blockplans sind die Objekte, die die Gruppe vertauschen kann, ohne die Struktur des Plans wesentlich zu ändern.
Jetzt müssten wir eigentlich tiefer einsteigen, um zu verstehen, was ein Wittscher Blockplan genau ist. Das wollen wir uns hier aber schenken. Stattdessen möchte ich eine sehr schöne Veranschaulichung der Mathieu-Gruppe \(\mathbb{M}_{12}\) zeigen, die ich bei John Baez M13, The n-Category Café: February 10, 2013 gefunden habe (die kleinste Mathieu-Gruppe \(\mathbb{M}_{11}\) kann man dann gut als Untergruppe von \(\mathbb{M}_{12}\) verstehen, indem man einen der 12 Punkte fixiert). Die Idee stammt laut John Baez aus Conway and Sloane’s Buch Sphere Packings, Lattices and Groups.
Die Struktur, dessen Symmetrie \(\mathbb{M}_{12}\) beschreibt, kann man sich als eine Ansammlung von 12 gleich großen Kugeln vorstellen, die sich als Kugelpackung um eine weitere gleich große Zentralkugel gruppieren und diese Zentralkugel berühren. Wenn wir die 12 Kugeln möglichst gleichmäßig auf der Oberfläche der Zentralkugel anordnen, dann liegen sie in den 12 Ecken eines Ikosaeders.
Da sich die 12 Kugeln nicht gegenseitig berühren, ist genug Raum vorhanden, um sie auf der Zentralkugel herumzurollen, sodass sie ihre Plätze ändern können. Dabei sollen sie aber immer die Zentralkugel berühren. Wir wollen die Kugeln also wirklich auf der Zentralkugel herumrollen und sie nicht einfach in die Hand nehmen, abheben und vertauschen. Das geht nur, wenn wir mehrere Kugeln gleichzeitig bewegen, und zwar so:
Wir suchen uns eine der 12 Kugeln heraus, halten sie fest und betrachten ihre 5 direkten Nachbarkugeln (die Zentralkugel zählen wir nicht dazu, denn sie bleibt immer im Zentrum des Kugelhaufens fixiert). Diese 5 Nachbarkugeln können wir nun im Uhrzeigersinn eine Position weiter um die zuvor ausgewählte Kugel herumrollen.
Die entsprechenden Bilder können Sie auf
M13, The n-Category Café: February 10, 2013
bewundern. Da die Bilder nicht als frei gekennzeichnet sind, verwende ich hier
das gleichwertige Bild des Ikosaeders, dessen 12 Ecken wir durchnummerieren.
Wir picken jetzt eine Ecke heraus und rotieren die Nummern der 5
Nachbarecken um die ausgewählte Ecke im Uhrzeigersinn herum, sodass diese 5 Ecken
anschließend neu nummeriert sind (den Ikosaeder selbst drehen wir dabei aber nicht –
es ist nur eine neue Ecken-Nummerierung):
Unter Verwendung von
Wikimedia: File:Icosahedron.svg<"a> von DTR,
CC BY-SA 3.0
Mit mehreren solcher 5-er-Rotationen hintereinander können wir jede gerade Vertauschung (Permutation) der 12 Kugeln bzw. Eckennummern erzeugen. Diese Gruppe kennen wir bereits: es ist die alternierende Gruppe \(A_{12}\). Um die kleinere Gruppe \(\mathbb{M}_{12}\) zu erhalten, mussen wir noch eine Einschränkung machen: Wir erlauben nur solche Veränderungen, bei denen wir zuerst 5 Kugeln (Eckennummern) um eine Kugel (Ecke) im Uhrzeigersinn herum rotieren und anschließend immer 5 (zumeist andere) Kugeln um deren Mittelkugel gegen den Uhrzeigersinn herum rotieren. Diese gepaarten 5-er-Rotation im und gegen den Uhrzeigersinn können wir ein oder mehrfach hintereinander ausführen und erhalten so die Elemente der Mathieu-Gruppe \(\mathbb{M}_{12}\). Diese Gruppe ist mit \( 8 \cdot 9 \cdot 10 \cdot 11 \cdot 12 = 95.040 \) Elementen um etwa das 2500-Fache kleiner als \(A_{12}\), die \( 12!/2 = 479.001.600/2 = 239.500.800 \) Elemente umfasst. Wir können mit den gepaarten 5-er-Rotation also nicht mehr jede beliebige gerade Vertauschung der Kugeln bzw. Eckennummern erzeugen.
Es ist also durchaus möglich, sich zumindest die kleinsten sporadischen Gruppen bis zu einem gewissen Grad zu veranschaulichen. Bei den größeren sporadischen Gruppen wird das allerdings immer schwieriger. Besonders schwierig ist es bei der weitaus größten von ihnen, der sogenannten Monstergruppe \(M\). Sie besitzt ungefähr \(8 \cdot 10^{53}\) Elemente – das ist ungefähr die Zahl der Atome des Gasriesen Jupiter.
Tatsächlich ist diese riesige Gruppe so etwas wie die Mutter der meisten sporadischen Gruppen. Immerhin sind 20 von ihnen (einschließlich der 5 Mathieu-Gruppen) Untergruppen der Monstergruppe (wobei man sie selbst mit dazuzählt). Man nennt diese 20 Gruppen auch die Happy Family. Die 6 Gruppen, die nicht zu dieser Happy Family gehören, nennt man Parias (Ausgestoßene oder Außenseiter).
Das es die Monstergruppe überhaupt gibt, vermuteten erstmals im Jahr 1973 die beiden Mathematiker Bernd Fischer und Robert Griess. Erst 9 Jahre später gelang es Griess dann, die Gruppe konkret zu konstruieren.
Sucht man nach einer Definition dieser wahrlich monströsen Gruppe, so findet man Sätze wie "Die Monstergruppe ist Galoisgruppe eines Polynoms mit rationalen Koeffizienten und kann durch Angabe dieses Polynoms vollständig charakterisiert werden" (Wikipedia). Mhhh... Ebenfalls auf Wikipedia fand ich die "Monstergruppe als Automorphismengruppe einer kommutativen, nicht-assoziativen Algebra auf einem 196.883-dimensionalen Raum". Auch schwierig, aber man ahnt die Komplexität. Besonders schön fand ich da den Wikipedia-Satz "It is difficult to give a good constructive definition of the monster because of its complexity."
Man kennt bis heute tatsächlich keinen einfachen Weg, die Elemente der Monstergruppe darzustellen. Dank Computerhilfe verfügt man immerhin über zwei invertierbare 196.882 mal 196.882 Matrizen mit Elementen aus dem Körper der Ordnung 2 (kann man sich als Bits 0 und 1 vorstellen mit \(1 + 1 = 0\)), die über die Matrixmultiplikation die Monstergruppe erzeugen. Im Computer belegt jede solche Matrix über viereinhalb Gigabyte, sodass praktische Rechnungen mit solchen Matrizen selbst auf modernen Computern ziemlich aufwendig sind. Mit einigen Tricks hat man da mittlerweile deutliche Fortschritte bei Computerrechnungen erzielt, aber anschaulicher wird die Monstergruppe dadurch auch nicht.
Vermutlich ist es gerade ihre enorme Komplexität, die dazu geführt hat, dass sich die Monstergruppe für die Mathematik als zunehmend wertvoll erwiesen hat. So fand man überraschende Zusammenhänge zu der sogenannten j-Funktion, einer Funktion in den komplexen Zahlen. Wie schon bei der Riemannschen Vermutung schaffen diese als monstrous moonshine bekannten Zusammenhänge zwischen der diskreten (und sogar endlichen) Monstergruppe und der kontinuierlichen j-Funktion eine tiefe Verbindung zwischen diskreter und nicht-diskreter Mathematik. Auf diese Weise ergeben sich sogar Querbezüge zur String Theorie, über die sich die moderne Physik ihren Kopf zerbricht.
Dass es die Monstergruppe gibt, scheint also angesichts ihrer faszinierenden Eigenschaften kein Zufall zu sein, auch wenn sich ihre Struktur nur schwer erfassen lässt. Aber selbst für die Experten ist sie immer noch ein zwar wunderschönes, aber zugleich zutiefst mysteriöses Objekt.
Literatur:
© Jörg Resag, www.joerg-resag.de
last modified on 13 May 2023